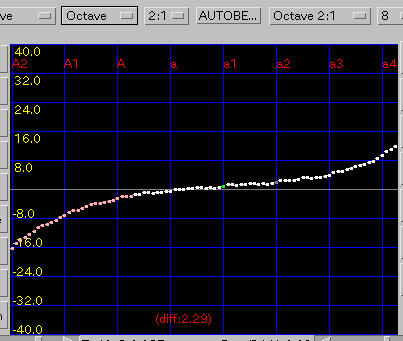
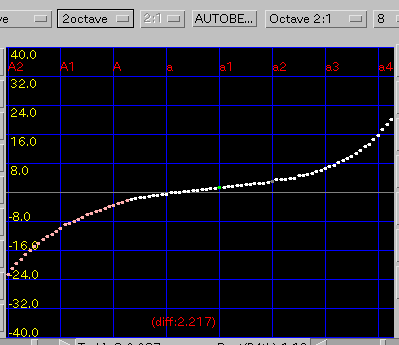
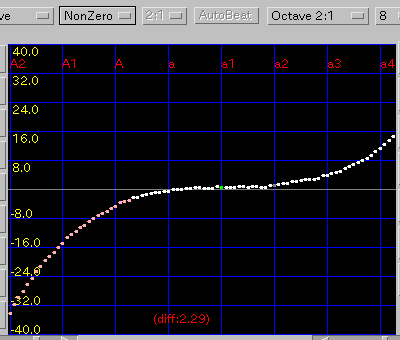
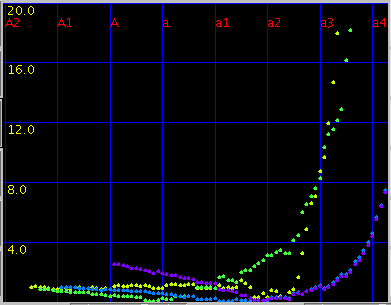
Octave: 1オクターブの`うなり'(2:1)を 0.5ぐらいで拡張します。
傾き(grade)を 0.08と 0.1にした場合です。
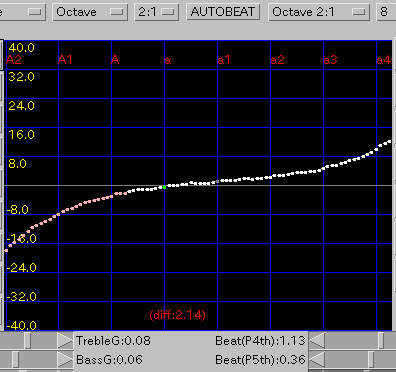
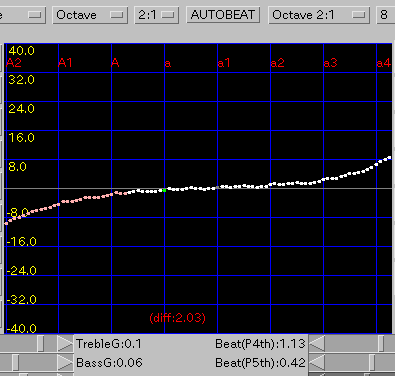
A(1)と C(88)のセント値の差は 30.2と 18.1です。
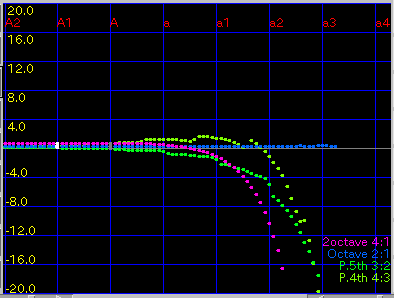
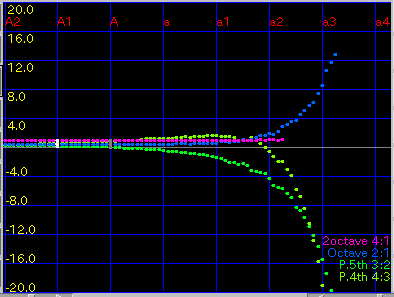
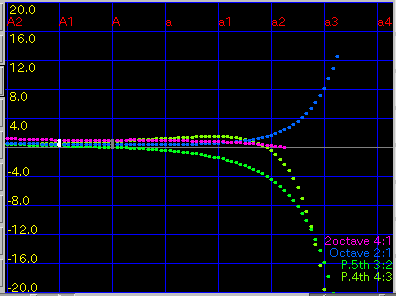
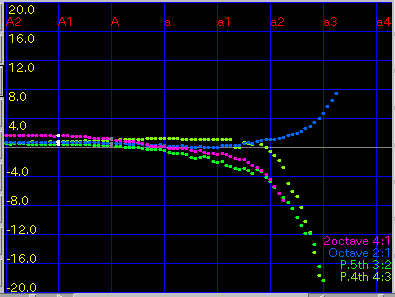
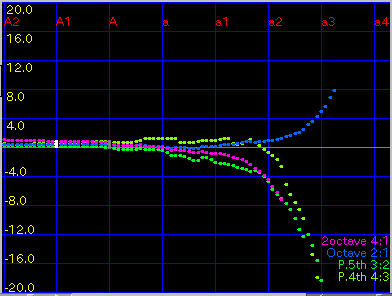
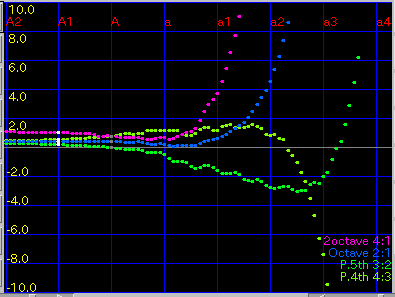
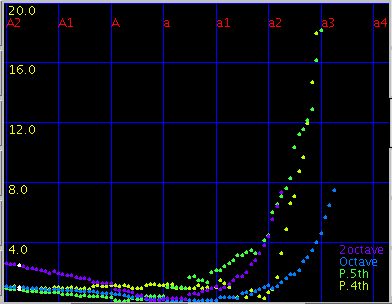
2Octave: 2オクターブの'うなり'(4:1)を
1.0ぐらいで拡張します。
傾き(grade)を 0.08と 0.1にした場合です。
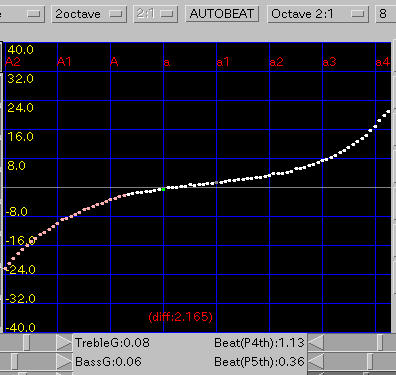

A(1)と C(88)のセント値の差は 43.4 と 29.3です。
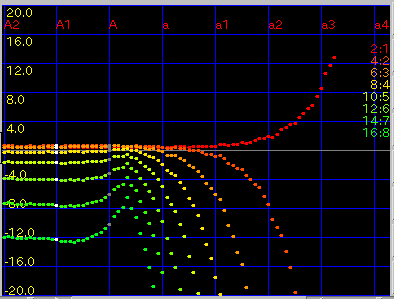
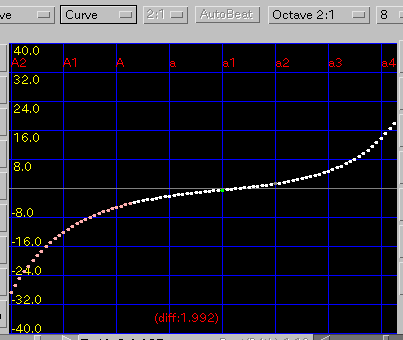
Curve: インハーモニシティ値を
cosh(双曲線余弦 - ハイパボリックコサイン)に対応させてから
sinh(双曲線正弦 - ハイパボリックサイン)と
-e(ネイピア数 - 自然対数)を足し合わせて
2オクターブの'うなり'を一定にする計算式の方法です。
参照〉
インハーモニシティの曲線から調律曲線を求める
(Inharmonicity curve to Tuning Curve)
参照〉
計算式から求める調律曲線のシミュレーション
(Formula Tuning Simulation)
傾き(grade)を 0.08と 0.1にした場合です。
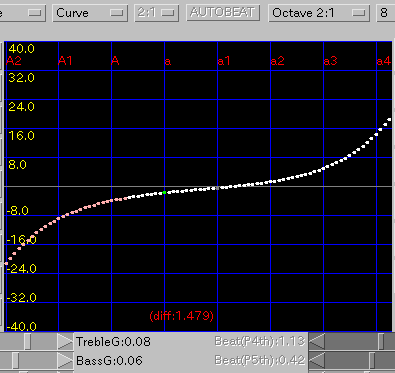
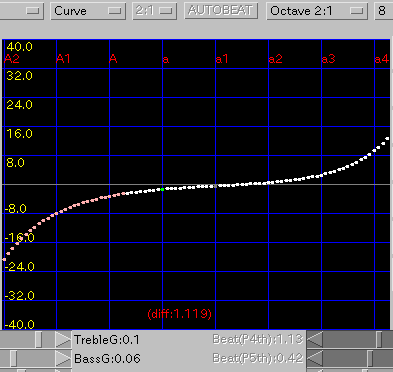
A(1)と C(88)のセント値の差は 46.9 と 42.9です。
NonZero: ノンゼロ方式です。
(これまでの「巻線の調律シミュレーション」と
「高音部の調律シミュレーション」を合わせた方法です。)
'うなり'を 0にするのではなく
倍音を同じぐらいに合わせると言う考え方です。
巻線部と高音部とでは合わせ方が異なります。
傾き(grade)を 0.08と 0.1にした場合です。
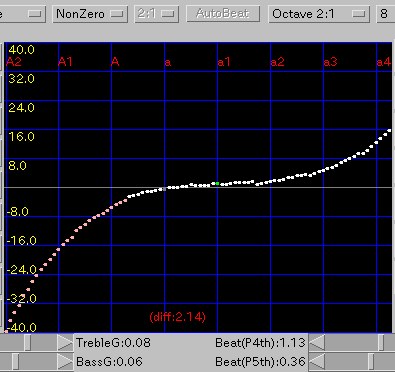
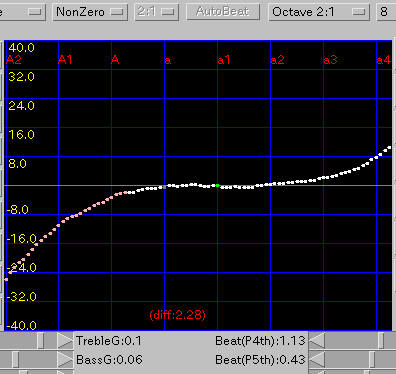
A(1)と C(88)のセント値の差は 55.4 と 36.5です。
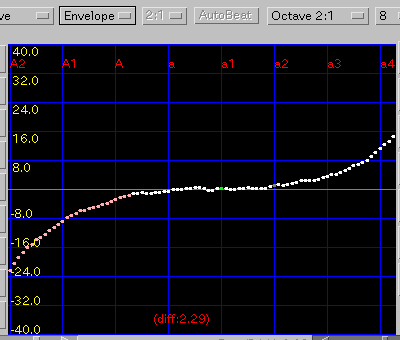
Envelope: エンベロープ方式です。
(v0.4.1)高音部もエンベロープ方式になりました。
ただあまり違いはありません。
また「NonZero」では殆んど固定ですが こちらは
倍音の取り方で低音域のカーブが変更出来るのが特徴です。
参照>
エンベロープのシミュレーション(Simulation of Envelope)
ここでは 10倍音
12倍音までに固定しています。
傾き(grade)を 0.08と 0.1にした場合です。
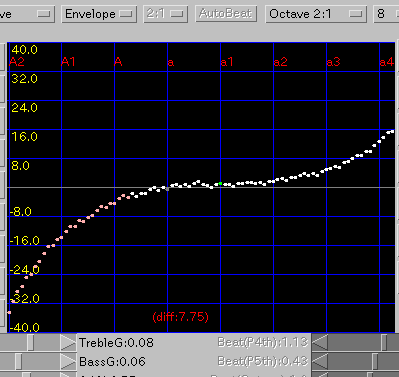
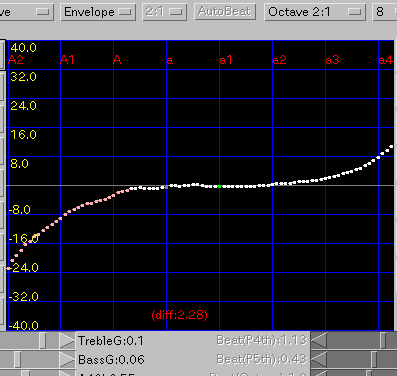
A(1)と C(88)のセント値の差は 50.2 と 33.6です。
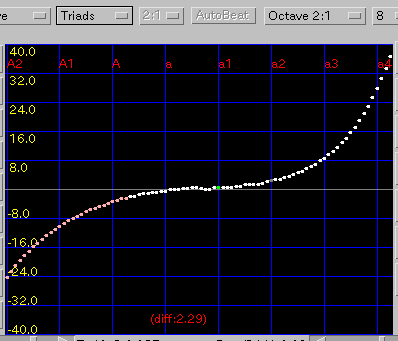
(※v0.5)Triads:三和音方式です。
「ベジエ曲線から調律曲線へ
(From Bezier to Tuning)」
からの方式です。
「純正5度と純正4度」などの二和音でも同様の効果がありますが
代表して「オクターブと純正5度と純正4度」の三和音を
載せています。
傾き(grade)を 0.08と 0.1にした場合です。
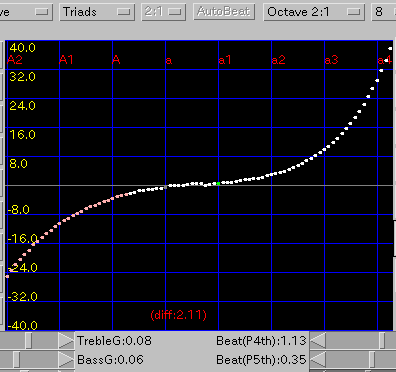
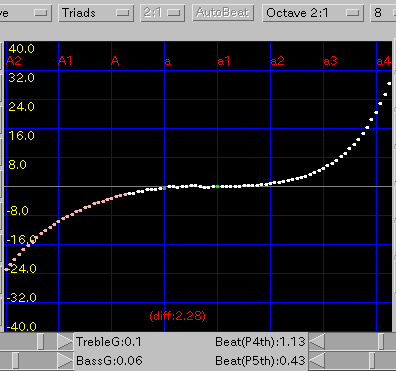
A(1)と C(88)のセント値の差は 62.7 と 51.5です。
例えば低音部の拡張を[Envelope]で[Beat]を拡大して見ます。
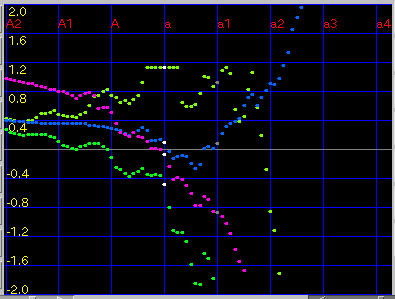
[Triads]ではより滑らかになっています。
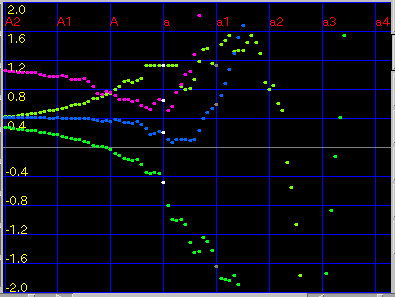
高音部の拡張を[Envelope]の[ABS][<-]では
オクターブと 2オクターブの 2つですが...
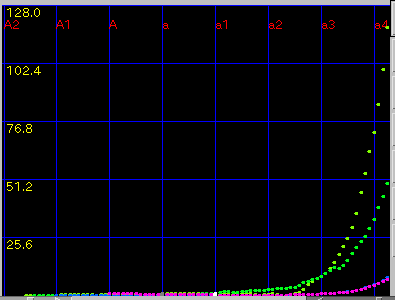
[Triads]では オクターブと 2オクターブと 純正4度の
3つまでが揃い...
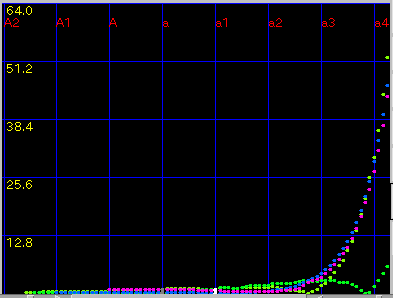
より実際の方法に近い様に思われます。
(ただ 高音部のセント値がより高くなる事については
未検証です。)
調律曲線を求める一つの試み
(Tuning Curve Pursuits)
で確かめてみました。
- 変更履歴:
- v0.6.4['18/07/15]
「HTML5版 調律シミュレーター」を追加しました。
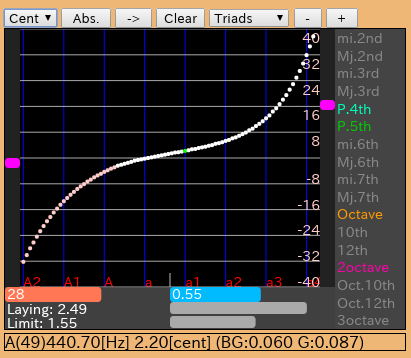
 HTML5版です。
HTML5版です。
- v0.6.3['17/02/05]
[Bend]ボタンを追加しました。
同時に[Bend]と[BendKey]のスラーダも追加しました。
それに合わせて MakeInharmonicity.java v0.2を改定しました。
- v0.6.2['16/11/13]
[Curve]以外で[Beat(P4th)][Beat(P5th)]スライダーの動作を可能としました。
ただ 値が大きく外れると制限が働きます。
- v0.6.1['16/08/28]
[Octave][2octave]の拡張の不具合を修正しました。
- v0.6['16/08/12]
[cent]値の表示から加えていたインハーモニシティ値を無くしました。
傾き(grade)が 0.08と 0.1の場合を加えました。
- v0.5['16/06/12]
[BassG]のスライダで Tuningしないエラーを訂正しました。
[fit(ting)]ボタンを無くしました。
TuningTriads(三和音[Triads])方式を加えました。
比較の為 Tuningの計算方法を(Curve以外)統一して
全体を見直しました。
[Triads]では インハーモニシティ値が大きく外れると
制限が働いて異常な値になる場合があります。
- v0.4.1['15/08/16]
エンベロープ方式に高音部にも適応しました。
スライダーの移動で[Wave][FFT][Enve.]が連動しないのを修正しました。
- v0.4['15/03/14]
5番目のTuningとしてエンベロープ方式を加えました。
それに伴って[Wave][FFT][Enve(lope)]表示などを追加しました。
[Cent]値表示を1倍のみに固定しました。
[BeatColor]のスライダを無くしました。
- v0.3.4['13/06/01]
BeatのスライダをP4thとP5thに分けて
割り振りの比率[5th:4th]のスライダを無くしました。
[BeatColor]のスライダを追加しました。
TuningNonZero.javaを見直しました。etc.
- v0.3.2['13/04/08]
Tuningで[Octave]のシミュレーションに
[4:2]と[6:3]の比を追加しました。
[Cent]値表示を倍音に対応させました。
- v0.3['13/02/13]
[Laying]スライダと[lay]ボタンを無くして
[WoundW]巻線数スライダを加えました。
Tuningのシミュレーション(TuningFormula2.java)を
catenary型に改定しました。
- v0.2['12/07/03]
[Beat]の表示を打弦点・響板の特性で輝度を変更する様に変更しました。
[0:Cent]を[調律のシミュレーション]の選択へ
[Clear]として移しました。
- v0.1['11/12/03]
ctofなどTuningの計算を見直しました。
(DebugData.javaを追加しました。)
- v0.0['11/06/05]
β版
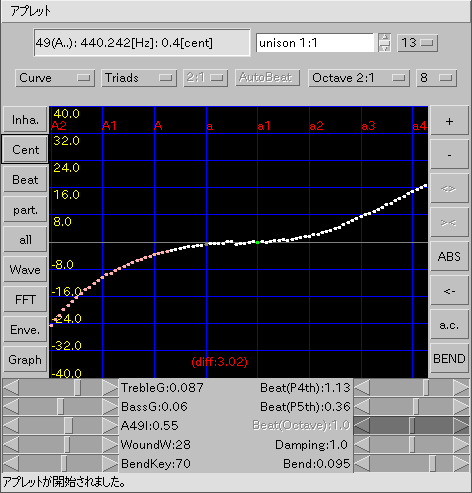
上段[ 49(A..): 440.693[Hz]: 0.55 ]テキスト表示:
カーソル位置のデータを表示します。
[ unison ... 3octave]リスト:
[Beat]で表示する音程を選びます。複数が可能です。
[ 15 ... 9 ]セレクタ:
FFTのサンプル数(2^x)を変更します。
[ Curve | Straight | Log ]セレクタ:
巻線部のインハーモニシティ値の傾き(Grade)を選択します。
- [Curve] はcoshの曲線で作ります。
- [Straight] は中音以上のキーと同じ 直線(指数)で作ります。
- [Log] は対数で作成しています。
[ NonZero | Octave | 2octave | Curve | Envelope | Triads
| ... ]セレクタ:
上記の調律のシミュレーションを選びます。
[Curve]での基準値はA49キーで 他はA37キーです。
[ ... | Clear ]すべてのキーのセント値を 0[cent]にします。
(その時 インハーモニシティ値は残ります。)
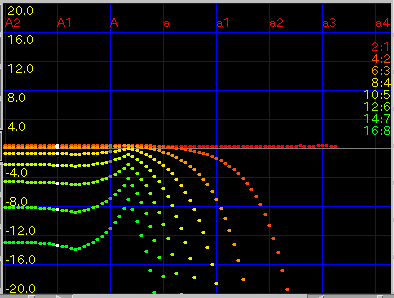
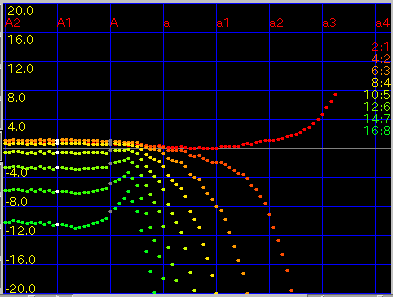
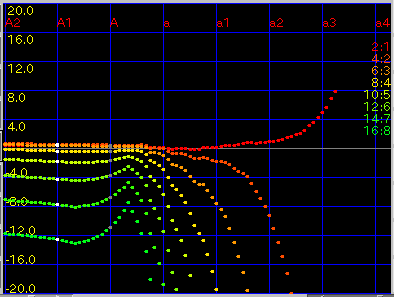
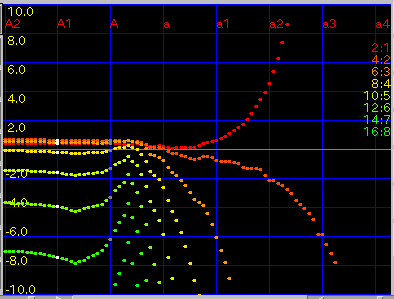
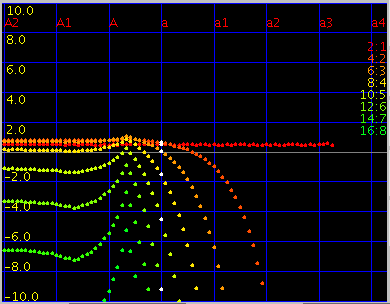
[ 2:1 | 4:2 | 6:3 ]セレクタ:
[Octave]の時に合わせる倍音を選択します。
[2:1]の時の[Cent]と[all(keys)]です。
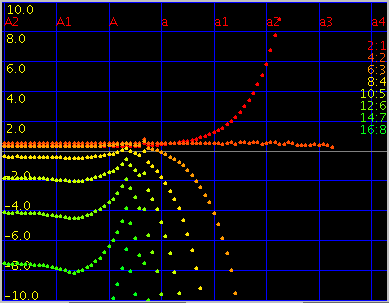
[4:2]の時の[Cent]と[all(keys)]です。
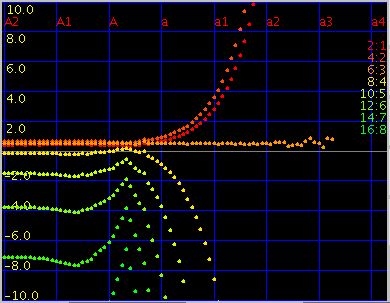
[6:3]の時の[Cent]と[all(keys)]です。
[ AutoBeat ]ボタン: [Octave | 2octave]の場合に
拡張する[Beat](うなり)の量を
割り振りから自動的に継るように設定します。
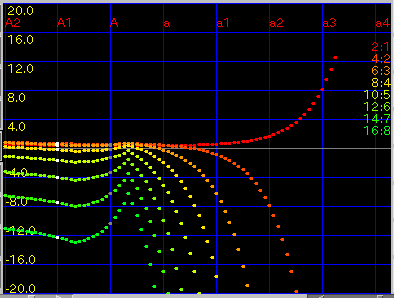
[ Unison 1:1 ... 3octave 8:1 ]セレクタ:
[part.]と[all]の時に表示する'うなり'の音程を選びます。
[ 1 ... 20 ]セレクタ: [part.]と[all]の時に
表示する倍音の最大値を選びます。
左側 [ Inha(rmonicity) ]ボタン:
インハーモニシティ値を表示します。
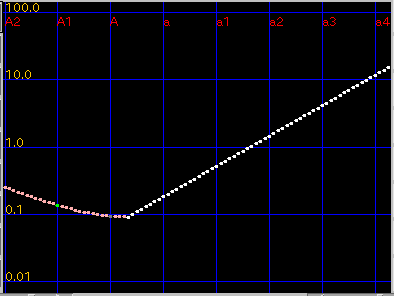
[ Cent ]ボタン: セント値を表示します。
(v0.6から) インハーモニシティ値を加えなくしました。
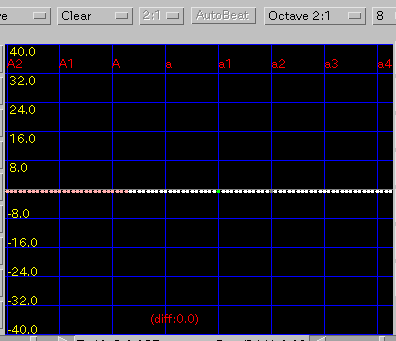
[ Beat ]ボタン: 音程のリストで選択した
'うなり'を表示します。
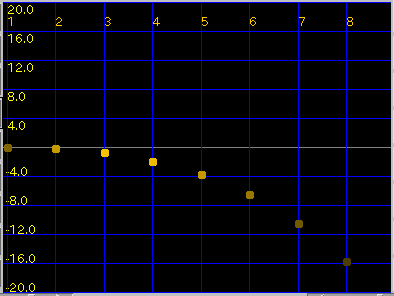
[ part(ial) ]ボタン:
カーソルが示しているキーの倍音の'うなり'を表示します。
その時に打弦点・響板の特性で輝度を変えています。
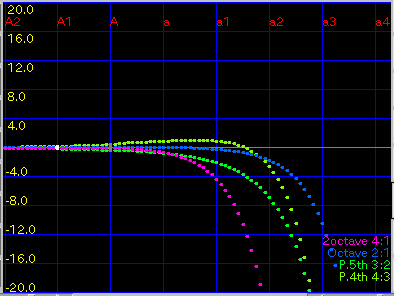
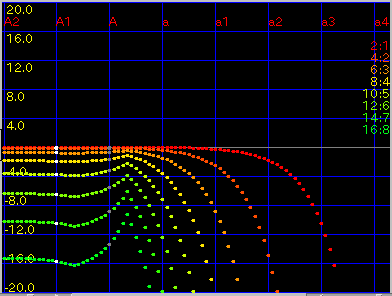
[ all (keys) ]ボタン:
音程のセレクタでの'うなり'を
すべてのキーで表示します。
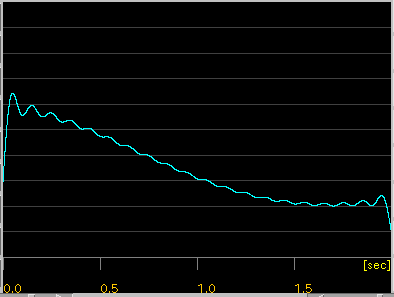
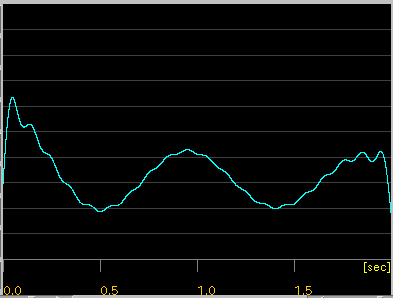
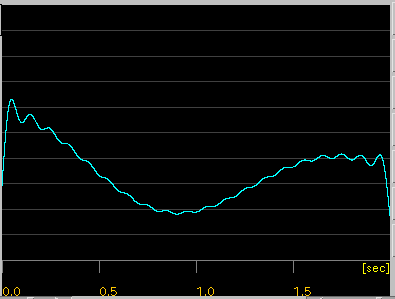
[ Wave ]ボタン:
カーソルキーとその音程から作成したWave信号を表示します。
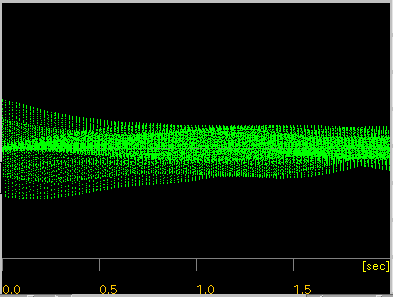
[ FFT ]ボタン:
Wave信号のFFTのスペクトルを表示します。
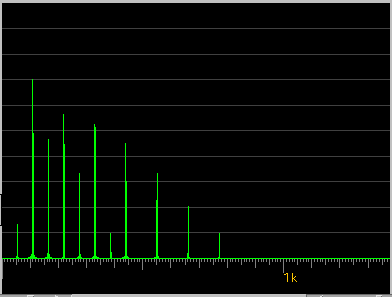
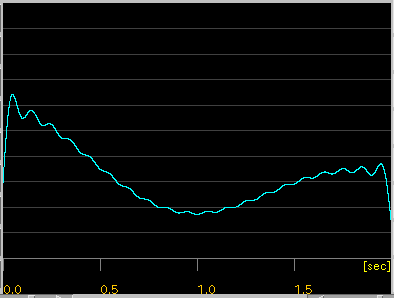
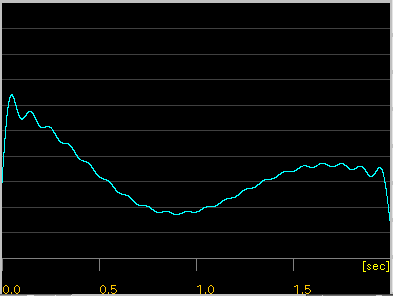
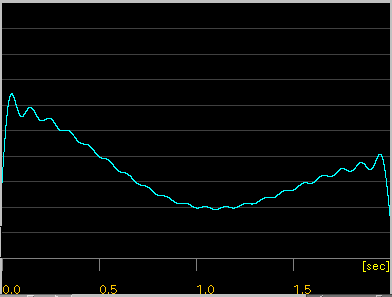
[Enve(lope) ]ボタン:
Wave信号からエンベロープ(包絡線)を取り出します。
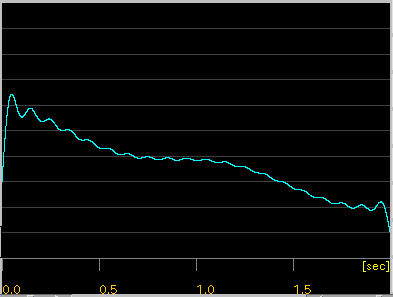
[ Graph | Text ]トグルボタン:
グラフ表示とテキストデータ表示を切替えます。
[Beat]で[ABS]の時は
割り振りの順番での'うなり'のデータを表示します。
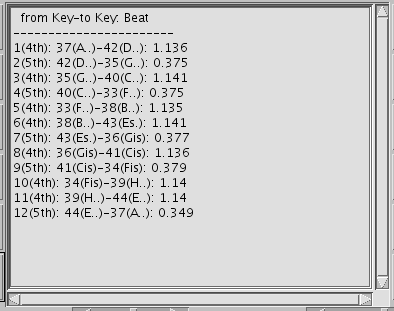
右側 [ + ][ - ]ボタン: 表示画面の上下の範囲を増減します。
[ >< ][ <> ]ボタン:
[FFT]の時に表示する周波数幅を増減します。
[ abs(olute) ]トグルボタン: [Beat][part.][all]での表示を
絶対値(absolute value)に切替えます。
[ -> | <- ]トグルボタン:
(v0.6)音程の取り方を [->]は下のキーから上のキーへ
[<-]は上のキーから下のキーへと切替えます。
[ a.c.(AutoCent) ]トグルボタン:
[Beat(P4th)][Beat(P5th)]スライダの時
割り振りのセント差が最小になる様に
自動的に'うなり'の量を調整します。
(※)[ Bend ]ボタン:
インハーモニシティ値の高音域を湾曲させます。
参照>
HTML5版 高音域のうなりについて
(HTML5 Above the High Range)
下段 [ TrebleG(rade): 0.087 ]スライダ:
中高音部の傾き(Grade - 直線)を変更します。
(以下左側の4つのインハーモニシティ値関係のスライダは
変更後Tuningのシミュレーションを行っていません。)
[ BassG(rade): 0.06 ]スライダ:
巻線の傾き(Grade)を変更します。
[ A49I: 0.55 ]スライダ:
A49キー(基準値)のインハーモニシティ値を変更します。
[ WoundW(ire):28 ]スライダ:
巻線の数(0~48)を変更します。
[ Beat(P4th):1.15 ]スライダ:
P4thの'うなり'の量を変更します。
[ Beat(P5th):0.4 ]スライダ:
P5thの'うなり'の量を変更します。
[ Beat(Octave): 1.0 ]スライダ:
割り振りから拡張する時の'うなり'の量を変更します。
調律のシミュレーションが[Octave | 2octave]の時に
[AutoBeat]ボタンをONにすると'うなり'は
自動的に合わせます。
[Damping:1.0 ]スライダ:
Wave信号の減衰値を変更します。(0.01~1.99まで変化します)
(※)[ BendKey: 70 ]スライダ:
インハーモニシティ値をこのキーまで湾曲させません。
(※)[ Bend:0.086 ]スライダ:
インハーモニシティ値の高音域を湾曲させます。
















 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)