CDの録音からJP(Java Pitch) で調律曲線を求めてみます。
インハーモニシティ値では中音ぐらいで済みましたが 最低音から最高音までの単音があり 録音日も近いもので 勿論同じピアノの使用であれば...との事で C(4)から B(86)まである ドビュッシーの「前奏曲集 第1巻」を選んでみました。
あるCDです。
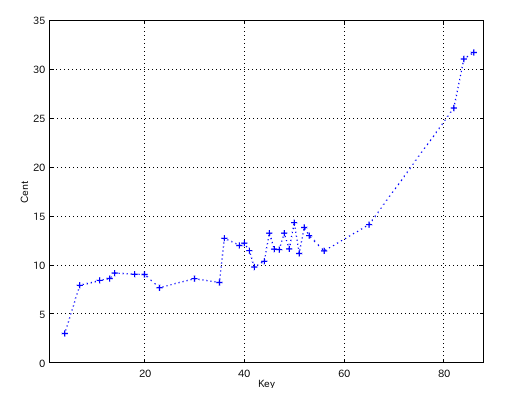
また別のCDです。
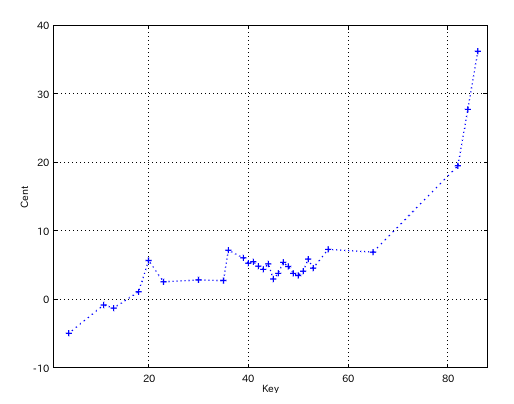
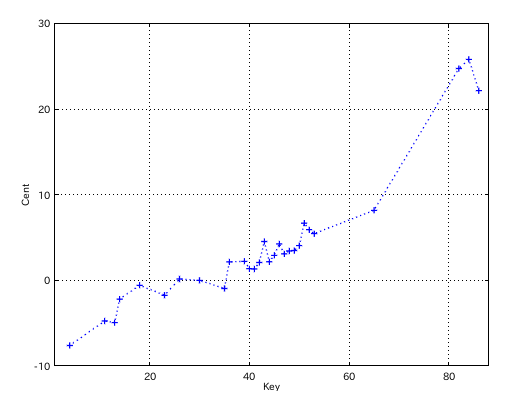
それらしい曲線は見受けられますが タッチの異なる演奏から 一定の音程を取り出す事は無謀です。
そこで ここでも"最小二乗法"を使用してみます。 今回の場合は 3次関数近似 での対応です。
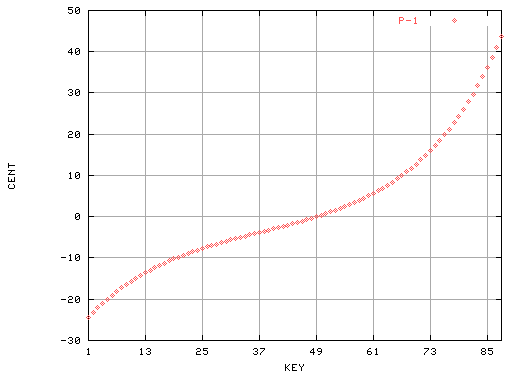
因みに 3次関数は y = a0 + a1 x + a2 x2 + a3 x3 と表される式で aを全て 1とすると 以下の様なグラフになります。
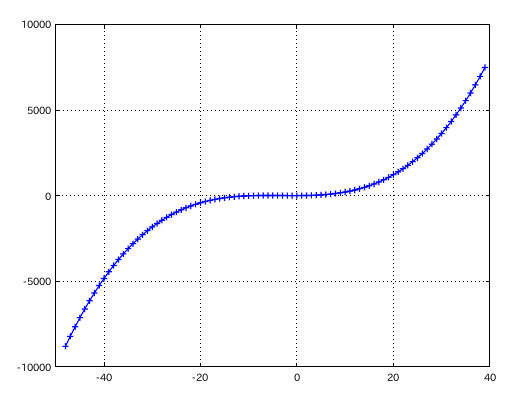
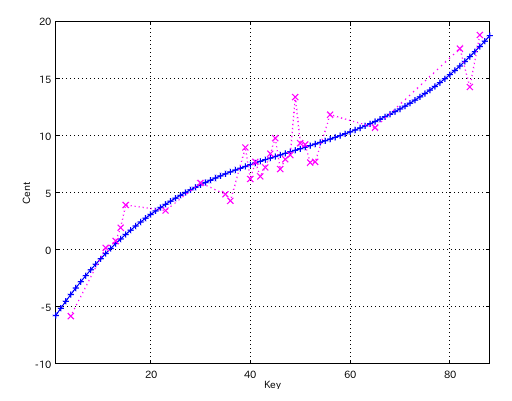
では 先のグラフを 最小二乗法で近似したグラフと表してみます。
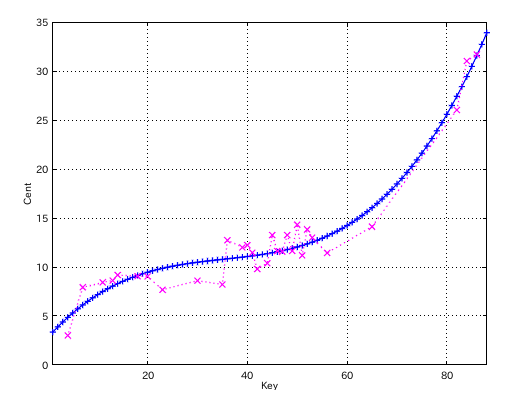
結果は以下になりました。
a0 = 2.7921
a1 = 0.57092
a2 = -0.014626
a3 = 0.000138
他のグラフの場合です。
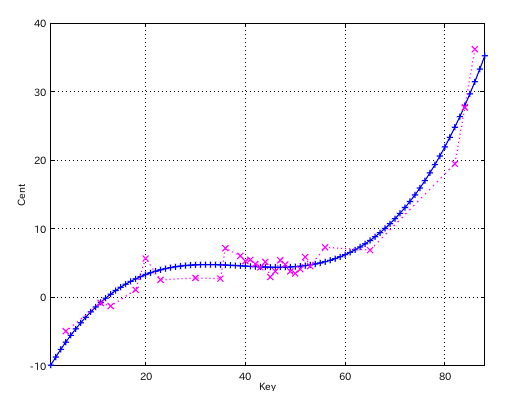
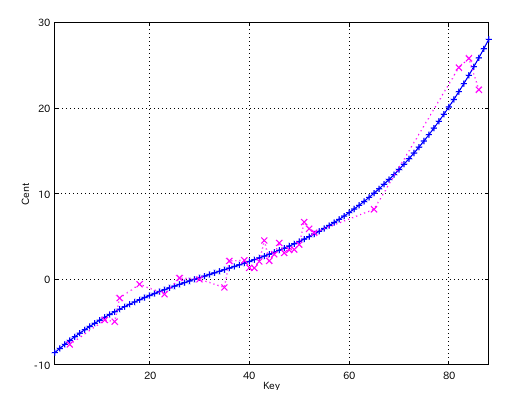
もっとも 明らかに 異常な測定値もありますので...
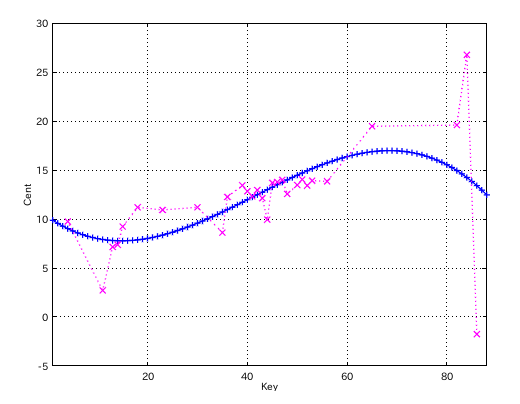
その場合は 異常値を削除してから再計算を行いました。
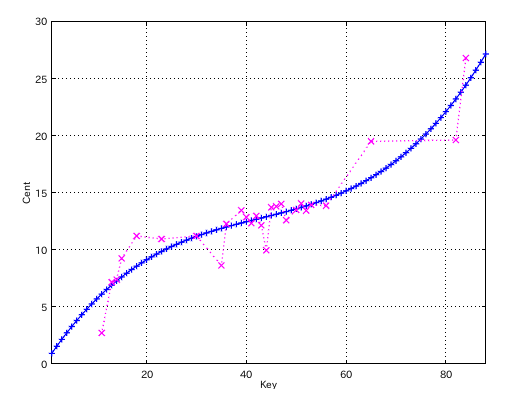
その A(1)と C(88)の[cent]値から
調律曲線の音程の差を取り出してみます。
測定誤差もありますが 20枚ほどの(1953年から2012年の)CDから
以下のような値となりました。
(v0.1.2) A(49)のインハーモニシティ値と 傾き(Grade)を加えました。
C(88)-A(1) [cent]: A(49)I. : Grade ---------------------------------- 45.183 : 0.6413 : 0.0973 26.235 : 0.6085 : 0.0811 36.607 : 0.5986 : 0.0833 30.889 : 0.6261 : 0.0892 32.526 : 0.5531 : 0.0844 28.402 : 0.5797 : 0.0881 47.140 : 0.6020 : 0.0892 46.098 : 0.6107 : 0.0829 24.525 : 0.5913 : 0.0820 46.355 : 0.6058 : 0.0888 37.173 : 0.5771 : 0.0808 62.803 : 0.4988 : 0.0775 43.731 : 0.4198 : 0.0756 37.783 : 0.5870 : 0.0831 34.012 : 0.6082 : 0.0897 26.860 : 0.6138 : 0.0837 60.285 : 0.6382 : 0.0931 34.819 : 0.5829 : 0.0912 42.752 : 0.6011 : 0.0870 30.625 : 0.5952 : 0.0885 30.599 : 0.6310 : 0.0921 31.130 : 0.6189 : 0.0866 51.639 : 0.5994 : 0.0887 47.475 : 0.6211 : 0.0894 ------------------------ 合計数 24
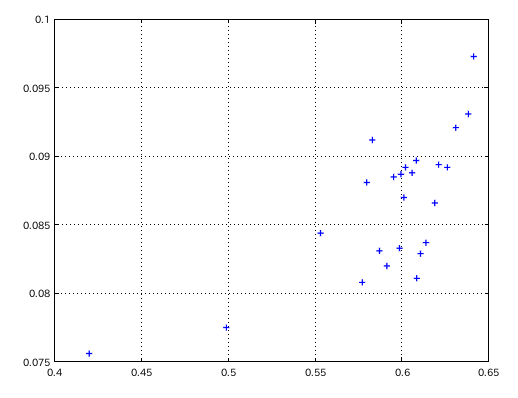
(v0.1.2) A(49)のインハーモニシティ値と 傾き(Grade)のグラフです。
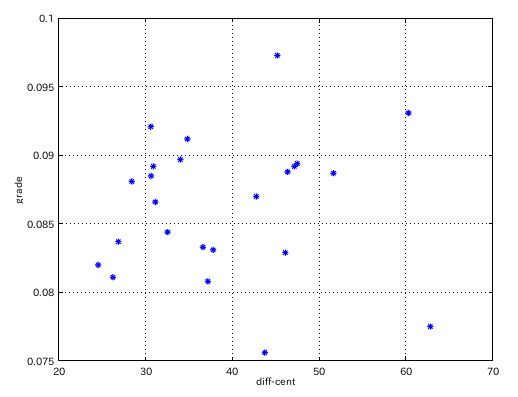
傾き(Grade)と セント差のグラフです。
因みに インハーモニシティ値と セント差のグラフです。
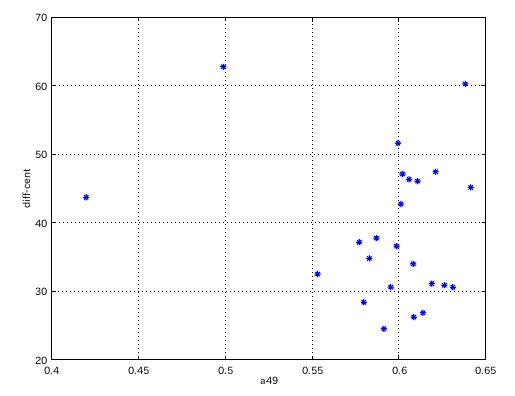
試しに"回帰分析"を行った所 "相関係数 (-1 ≦ R ≦ 1)"は 傾き(Grade)とは 0.060778 A(46)とは -0.177938 と 適合度は小さいですが それだけ 自在な様にも見受けられます...
セント差を 6段階のヒストグラムで表してみます。
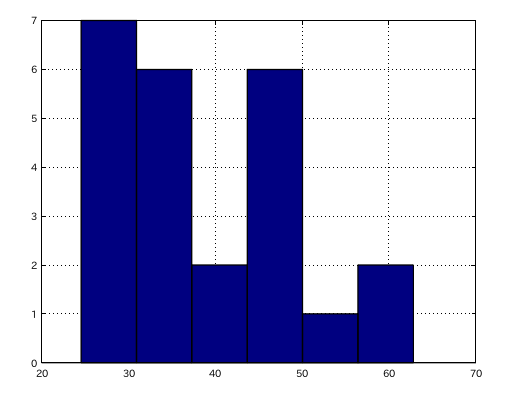
10段階のヒストグラムで表してみます。
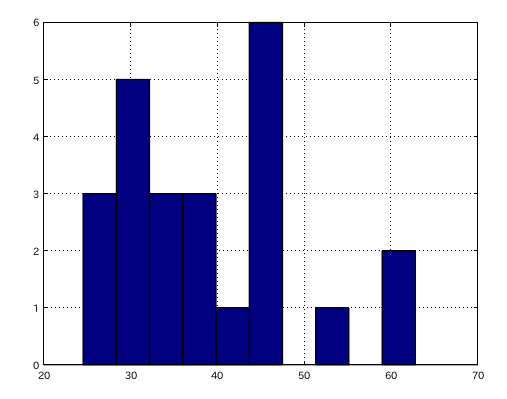
もう少し細かい 14段階にしてみます。
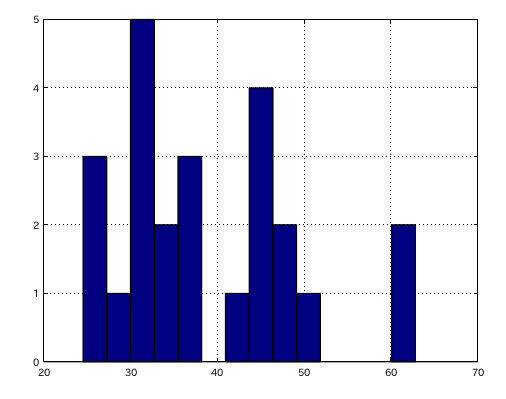
その中から 小さな値のグラフです。
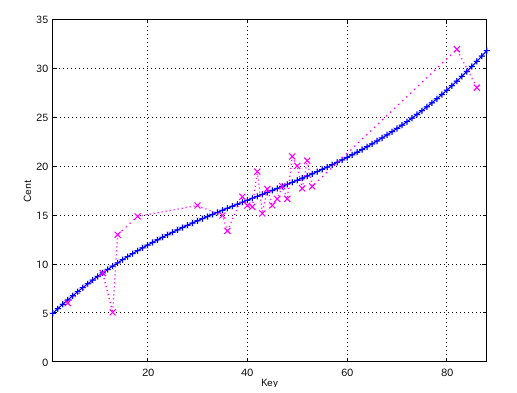
また 大きい値のグラフです。
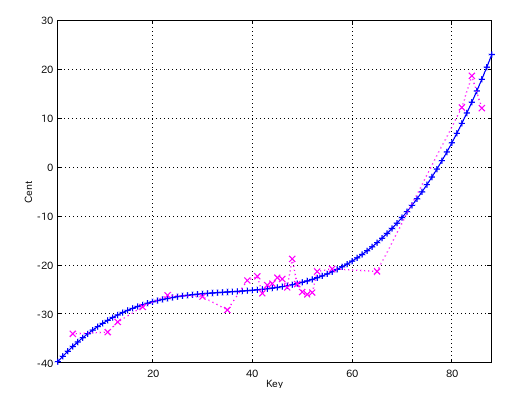
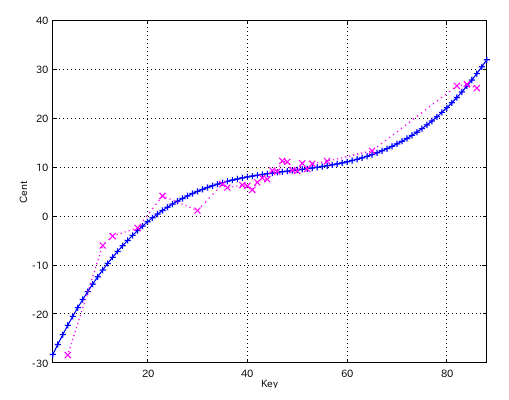
そこで ハタと考え込んでしまいました。
それに インハーモニシティ値は加えるのだろうか...
一緒に測定してるのだから それを加えればいいのではないか...
...しかし測定値に インハーモニシティ値を加えることは あり得ません。
では 何故これまで 調律曲線のシミュレーションに インハーモニシティ値を加えて来たのかと 云えば あの グラフに近付ける為 ではなかったか...
平均律のチューニング (Equal temperament tuning)/使い方(Usage)/調律曲線
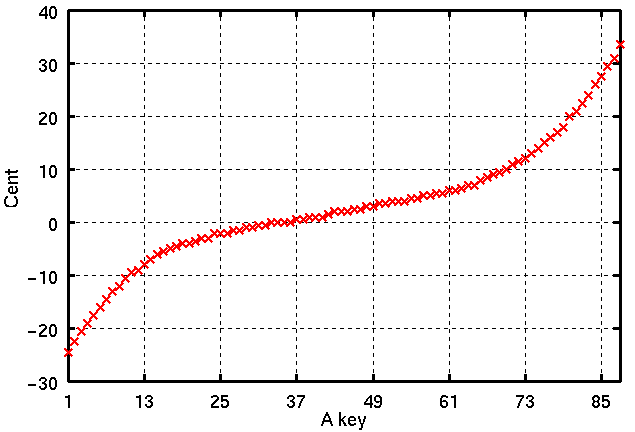
(v0.1.1)インハーモニシティについて (Inharmonicity)/「ピアノの調律曲線」
そうして これまで繰り返した インハーモニシティ値のシミュレーションと今回の実測から 調律曲線の音程差には 幅がある と云う事が 確認出来た様に思われます。
ではJava 調律シミュレーター
(Java Tuning Simulator)
から セント値に
インハーモニシティ値を加えずに表示して見ます。
始めは 0[cent]の場合です。
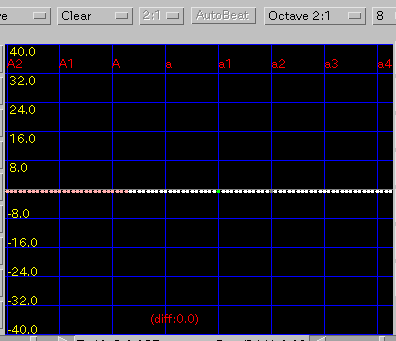
オクターブ・2オクターブ・カーブ の順です。
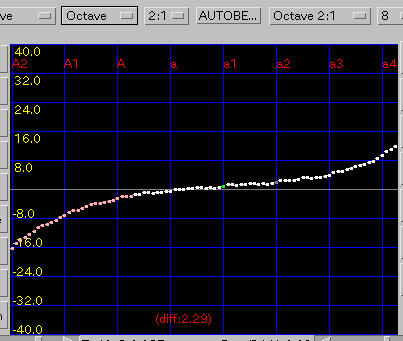
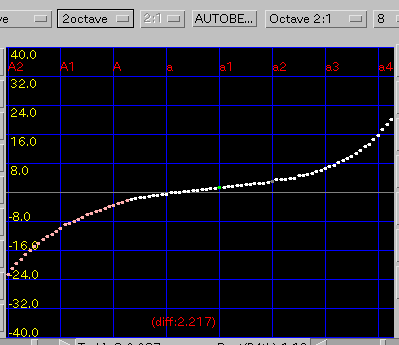
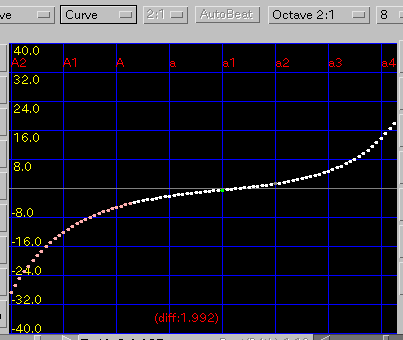
ノンゼロ・エンベロープ・3和音 の順です。
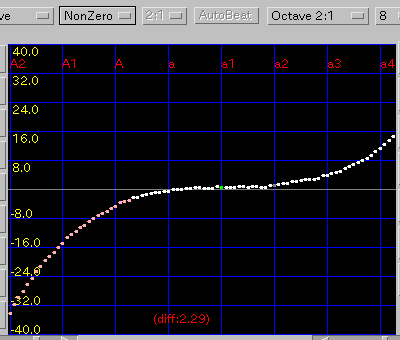
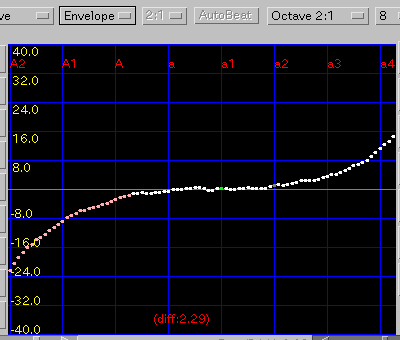
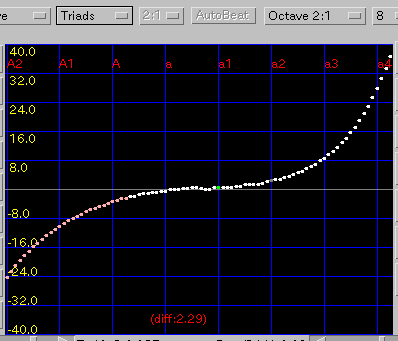
これで 3和音型の値が "異常に大きい" から ただの "大きい" に変わりました。
順次 Tuningのシミュレーションを 見直して行く予定です。
(変更履歴: