「白と黒で
(On the Keyboard) v0.8」を使用した ある条件での
オクターブ(A37-A49)の`うなり'です。
2:1です。
4:2と 6:3です。
2:1,4:2,6:3 共に`うなり'が見えません。
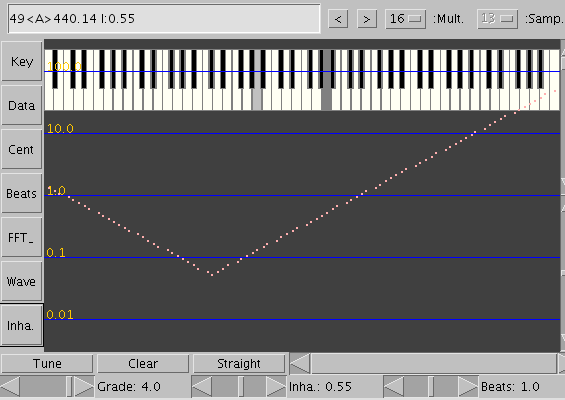
画面の設定は「Straight」(直線のインハーモニシティ)で
「Clear」(セント値を 0)・「Grade」(傾き)を 4.0とします。
そのインハーモニシティ値とセント値です。
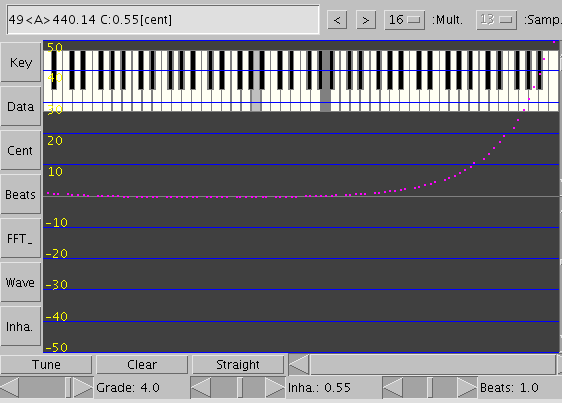
その時の 4度(A37-D42)と 5度下(A37-D30)です。
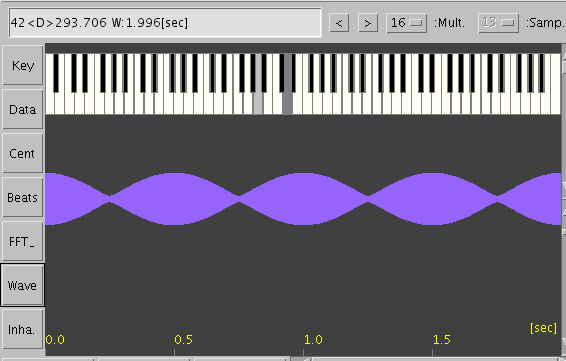
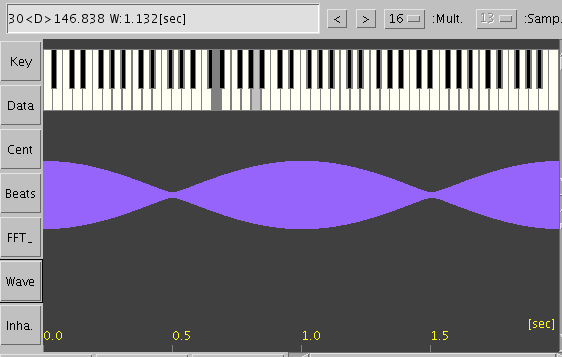
「インハーモニシティの傾き (Igrade)」で 上と同じ条件にして
それぞれの キー毎での倍音の`うなり'を見てみます。
「Straight」を選択・「Flat」でセント値を 0・
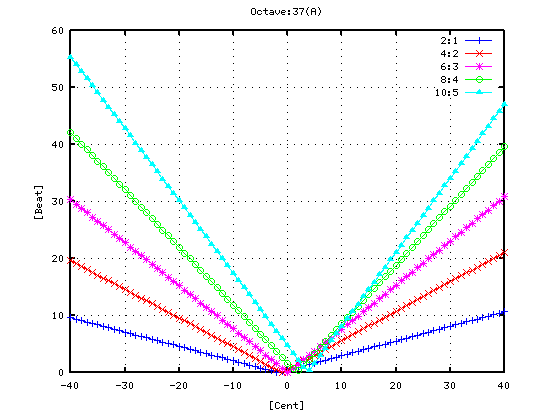
「Grade」を 4.0としてオクターブを見てみます。
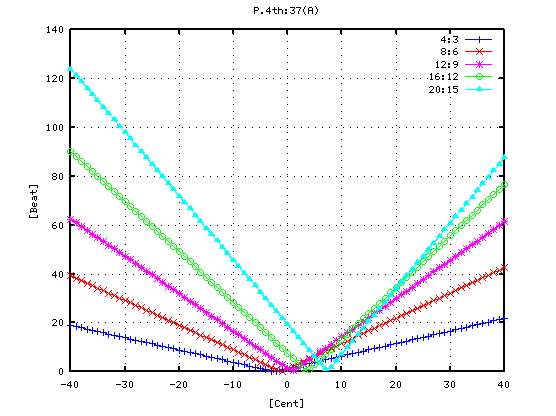
4度と 5度下です。
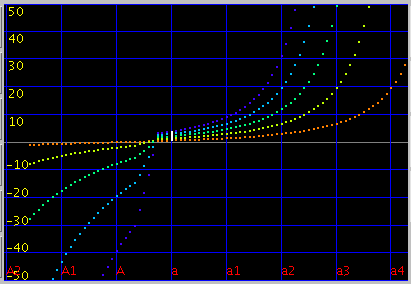
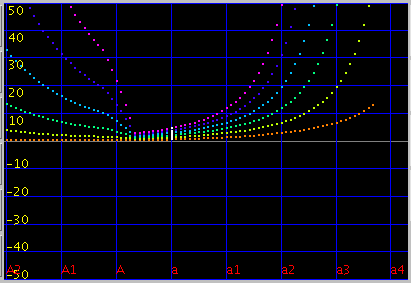
オクターブは 芯線部では`うなり'が 0になりますが 4度・5度ではそうならないように見えます。
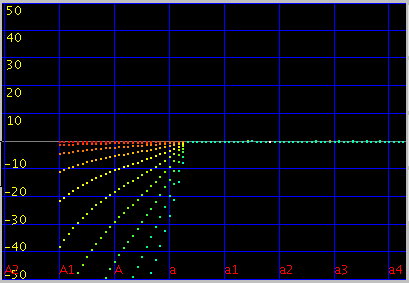
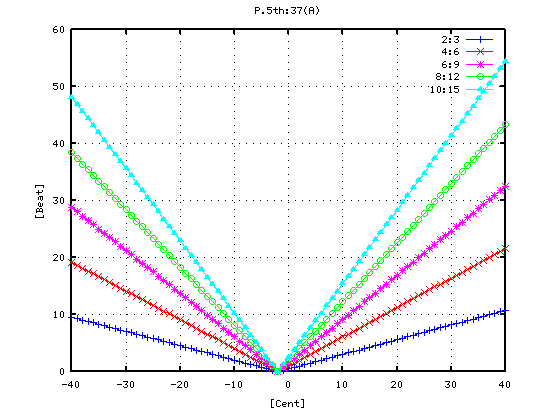
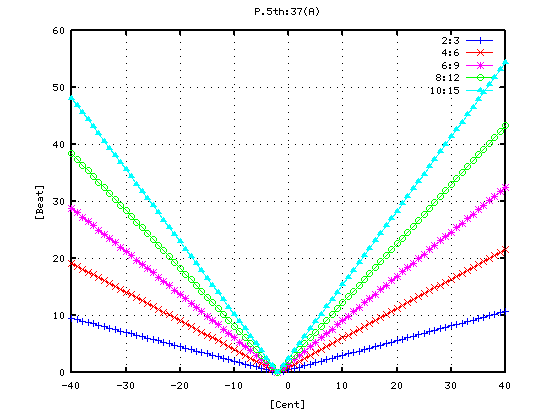
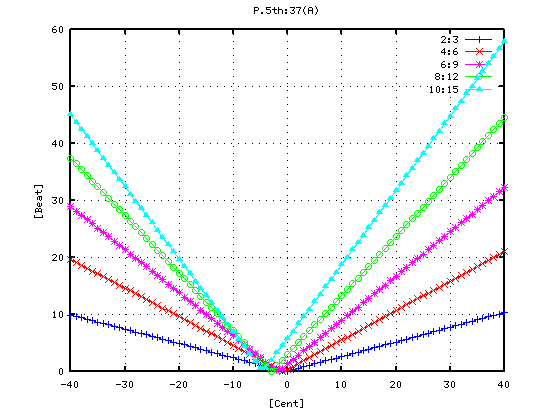
ではその時の オクターブ(A37-A49)で
片方のキーのセント値を変化させた場合の`うなり'を見てみます。
(A49の周波数を -40から +40まで 1[cent]づつ変化させた時の
倍音---ここでは 10:5まで---の`うなり'の数を表します。)
参照〉 Octave/第6回 Key Beats (平均律)
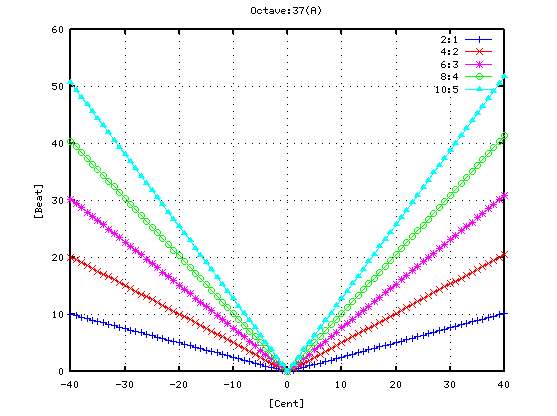
その時の 0[cent]での周波数です。
倍数: A49x1 [Hz] : A37x2 [Hz] : 周波数差 ----------------------------------------- 1 440.14 440.14 7.8848e-07 2 881.12 881.12 6.3138e-06 3 1323.8 1323.8 2.1343e-05 4 1769.0 1769.0 5.0704e-05 5 2217.5 2217.5 9.9314e-05 -----------------------------------------
周波数のセント値をグラフにしてみます。
倍数:周波数[Hz]:セント値[cet]:補正値[cent]:補正後[cent] -------------------------------------------------------- 1 440.14 0.550760 0.0 0.550760 2 881.12 2.201988 0.0 2.201988 3 1323.80 6.931696 -1.9550 4.976696 4 1769.00 8.830343 0.0 8.830343 5 2217.50 0.030411 13.6863 13.716711 --------------------------------------------------------
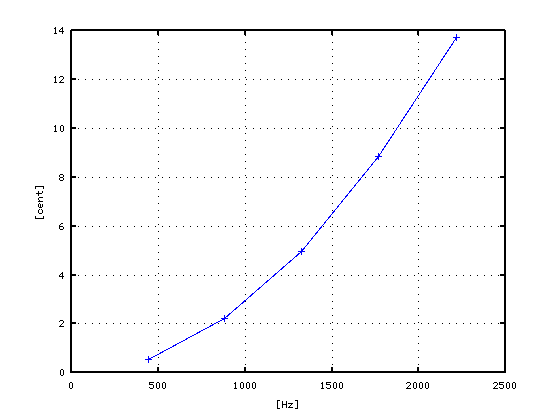
倍音には確かにインハーモニシティがあります。
4度の場合です。
倍数: D42x3 [Hz] : A37x4 [Hz] : 周波数差 --------------------------------------- 1 882.12 881.12 0.99811 2 1771.0 1769.0 2.0191 3 2673.5 2670.4 3.0864 4 3596.5 3592.3 4.2244 5 4547.5 4542.0 5.459 ---------------------------------------
5度下の場合です。
倍数: D30x3 [Hz] : A37x2 [Hz] : 周波数差 ---------------------------------------- 1 440.64 440.14 0.49763 2 882.12 881.12 0.9981 3 1325.3 1323.8 1.5043 4 1771.0 1769.0 2.0191 5 2220.1 2217.5 2.5454 ----------------------------------------
4度と5度は 0セントではない所で`うなり'が 0になっています。
参考までに 曲線のインハーモニシティで
傾き 0.087(2√2)・Tuningをシミュレーションした場合です。
オクターブです。
参照〉 Octave/第8回 Key Beats (Inharmonicity)
倍数: A49x1 [Hz] : A37x2 [Hz] : 周波数差 --------------------------------------- 1 440.14 439.7 0.43774 2 881.12 880.59 0.53381 3 1323.8 1323.8 -0.056066 4 1769.0 1770.7 -1.6814 5 2217.5 2222.2 -4.6998 ---------------------------------------
4度です。
倍数: D42x3 [Hz] : A37x4 [Hz] : 周波数差 -------------------------------------- 1 881.84 880.59 1.25 2 1771.9 1770.7 1.2672 3 2678.6 2679.8 -1.2225 4 3610.6 3618.2 -7.5783 5 4576.8 4596.1 -19.29 --------------------------------------
5度下です。
倍数: D30x3 [Hz] : A37x2 [Hz] : 周波数差 --------------------------------------- 1 439.8 439.7 0.10101 2 881.05 880.59 0.46684 3 1325.2 1323.8 1.3649 4 1773.7 1770.7 3.0681 5 2228.1 2222.2 5.8571 ---------------------------------------
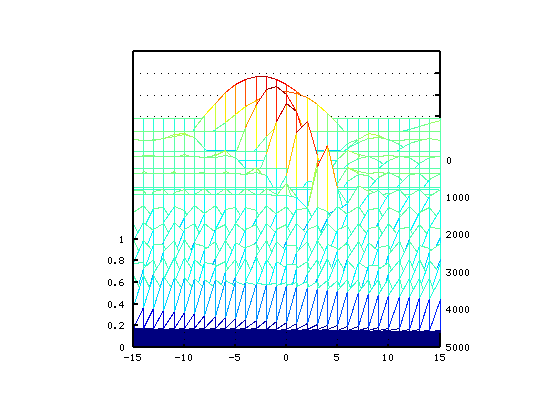
では 片方のキーのセント値を変化させた Wave信号の FFTスペクトルを並べて 立体(3D)化して見てみます。
セント値は左から右へ -15から+15へ 1[cent]づつです。
周波数は奥から手前へ 0から5000(7000|4000)[Hz]です。
順に オクターブ・4度・5度下です。
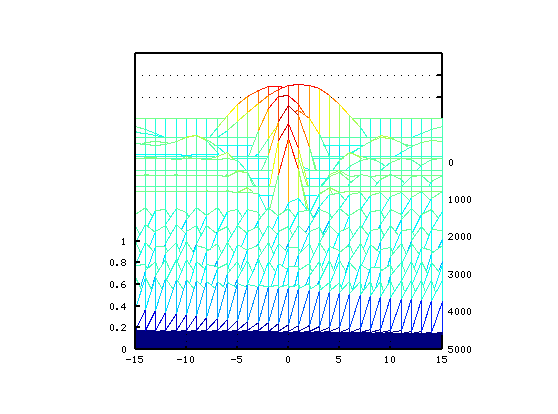
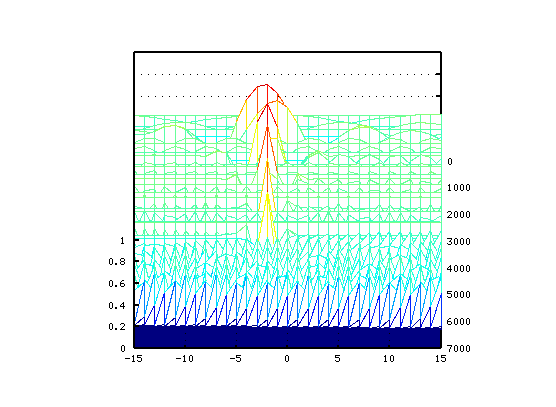
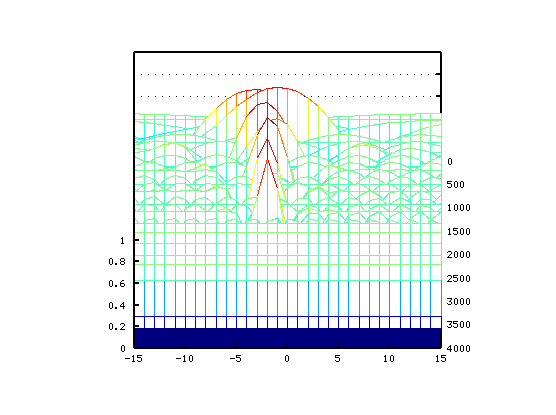
Tuningを行う時の聞こえ方は このようになるかと思われます。
参考までに 曲線のインハーモニシティで
傾き 0.087(2√2)・Tuningをシミュレーションの場合です。
順に オクターブ・4度・5度下です。
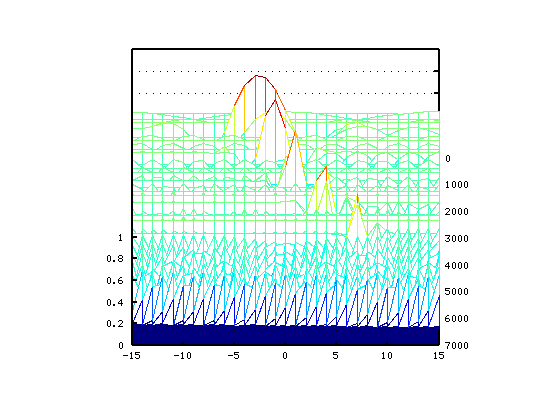

直線の傾き(Grade) 4.0のインハーモニシティのピアノを造れば 単音の倍音には インハーモニシティがあるのに 和音では インハーモニシティが無いかの様に(平均律 ?) 全ての倍音が 同時に共鳴する響きがすると思われます。
傾き(Grade)が 曲線の 0.087(2√2)と 直線 4.0のインハーモニシティ値を比べてみます。
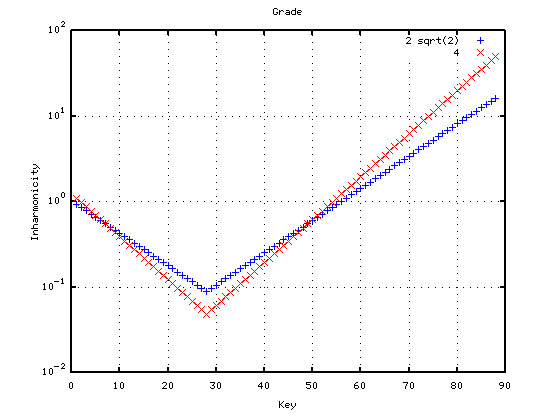
その時のセント値は 曲線の 0.087(2√2)では Tuningのシミュレーションを行っていて 直線 4.0では行わないのでインハーモニシティ値そのままとなります。
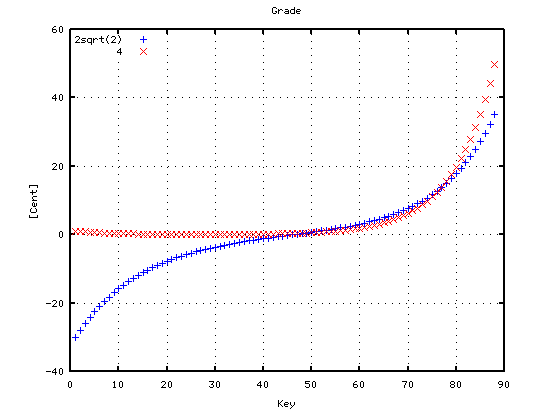
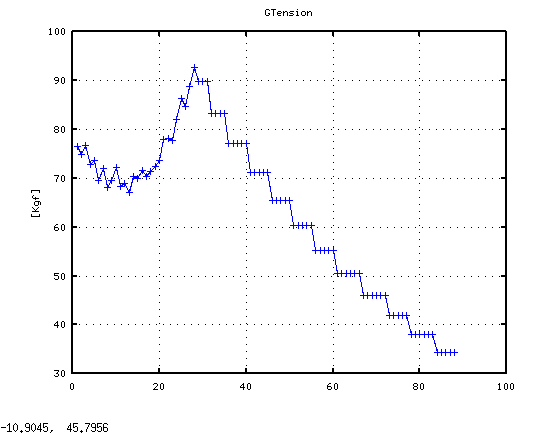
試しに弦長などを計算してみました。順に弦長・番手・張力です。
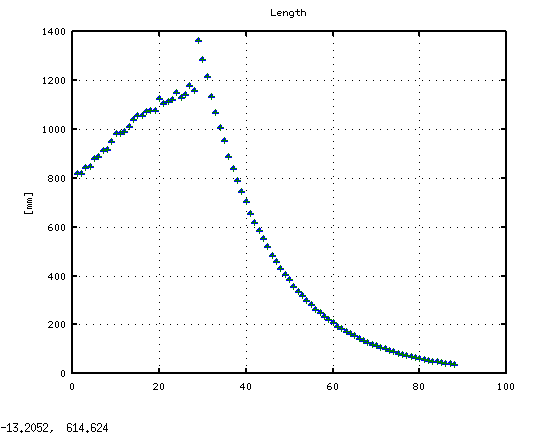
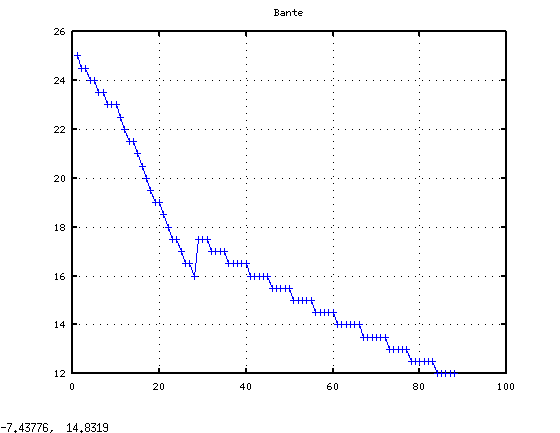
弦の最長は 1364.19[mm] 最短は 38.46[mm]。
番手は 25〜12番。あり得ない値ではありません。
ただし 張力は一定ではなく 95〜30[kgf]なので
鉄骨などの設計は難しいかも知れませんし、
調律もしづらいかも知れません;
メーカーさん 如何がでしょう?
変更履歴:
v0.1['10/09/26]