第8回 Key Beats (Inharmonicity) #8

インハーモニシティのある場合です。
2キー間で 片方のキーを変化させた時の 倍音の“うなり”の変化を見てみます。

function dispIKbeats(key, inte)
  global Inha Cent KB;
  KB = 88;
  grade = 0.087;
  Inha = makeCurve(28, 0.55, grade);
  Cent = tuning_c(Inha, 1.0, grade);

  multiple = 1:5;   # 倍音の範囲
  widec = 30;       # ±セント値の範囲
  [ratio rstr]= Interval(inte);
  for m = multiple
    ra = [ratio(2:3)*m inte];
    be = abs(getIKbeat(key, ra, -widec:widec));
    str = strcat(';P-', num2str(m), ';-@', getCP(m));
    plot(-widec:widec, be, str)
    hold on
  end
  hold off
  title(rstr)
  xlabel('[cent]')
  ylabel('Beat')
  grid on
end

function beat = getIKbeat(key, ratio, cent)
  freq1 = getIFrequ(key, ratio(1));
  freq2 = getIFrequ(key+ratio(3), ratio(2));
  freq2 = ctof(freq2, cent);
  beat = freq2-freq1;
end

function [inter, intst] = Interval(inte) # v0.2
  intn = [0 1 1; 1 16 15; 2 9 8; 3 6 5; 4 5 4; 5 4 3; 6 7 5;\
          7 3 2; 8 8 5; 9 5 3; 10 7 4; 11 15 8; 12 2 1;\
          16 5 2; 19 3 1; 24 4 1; 28 5 1; 31 6 1; 36 8 1];
  ratio = {'Unison' 'mi.2nd' 'Mj.2nd' 'mi.3rd' 'Mj.3rd' 'P.4th' 'Dim.5th'\
           'P.5th' 'mi.6th' 'Mj.6th' 'mi.7th' 'Mj.7th' 'Octave'\
           '10th' '12th' '2octave' 'Oct.10th' 'Oct.12th' '3octave'};

  inter = -1; # not
  intst = '';

  x = find(intn(:, 1) == abs(inte));
  if (x > 0)
    if (inte > 0)
      inter = intn(x, 1:3);
    else
      inter = [intn(x,1) intn(x,3) intn(x,2)];
    end
    intst = ratio{x};
  else
    usage("Interval([0-36]) -> [interval low high][name]");
  end
end

dispKbeats1.m と getKbeat.mの一部を改造して dispIKbeats.m と getIKbeat.mとして 他はそのまま使います。

Interval.m は キー間隔のマイナスに対応させました。

Tuningのシミュレーションを行ってから 2キー間の倍音の“うなり”の変化を見てみます。

> dispIKbeats(37, 5)

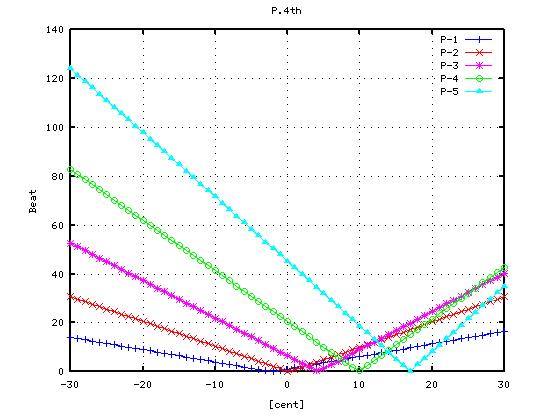
37Aキーの 4度上です。

> dispIKbeats(37, -7)

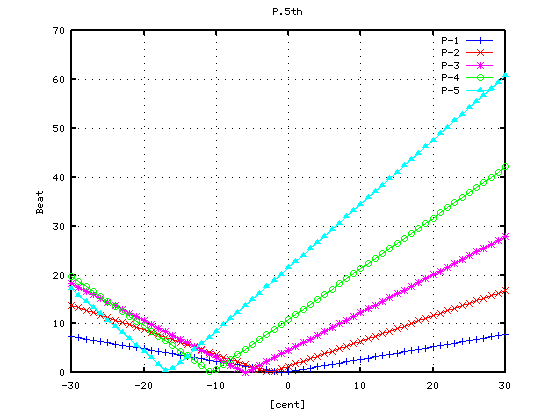
37Aキーの 5度下です。

> dispIKbeats(37, 12)

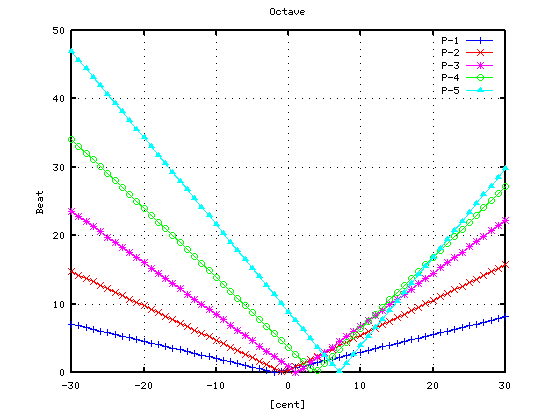
37Aキーのオクターブ上です。