 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
「I, grade. 我輩は"傾き"である。しかし、名前は まだ 無い。」
インハーモニシティ(Inharmonicity)は 弦の性質から個々のキーで表現されるものですが それに対して キー同士又キー全体のインハーモニシティの 勾配(grad)・傾斜(gradient)を 直線的でも曲線的でも (対数グラフでなければ どちらも曲線的ですが ここではY軸(上下方向)対数グラフでの比較で表現しています) 取り合えず 傾き(grade)と呼びます。
インハーモニシティの傾き(grade)をシミュレーションして 音程間の`うなり'(響き)を見てみます。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
(※変更履歴:
v0.4['16/09/18]
[Cent]表示からインハーモニシティ値を加え無くしました。
v0.3.3['15/07/06] javaScript部分を別にしました。
v0.3.2['14/01/25]
「曲線の傾き(grade)」に
HTML5版を追加しました。
v0.3.1['13/02/10] Tuningのシミュレーション(TuningFormula2.java)を
catenary型に改定しました。
v0.3['13/01/12] [Grad.]表示を加えました。
画面の構成を変更しました。cssファイルを別にしました。
v0.2['10/09/15]
[Tune]と[Flat]ボタンをトグルボタンに変更しました。
[Straight]の Tuningを無くしました。
[grade]の値を
[Curve]と[Straight]で変えるように変更しました。
v0.1['09/03/17]
v0.0['08/06/15])
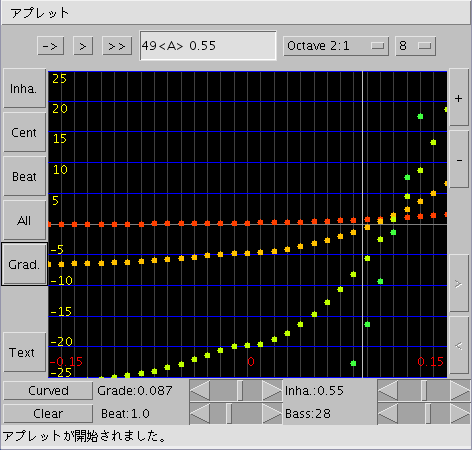
上段(※)[ -> | <- ]トグルボタン: 音程キーを上向き/下向きで切替えます。
[ > | < ][ >> | << ]ボタン: 現在のキー位置を 1つ 又は オクターブで移動します。
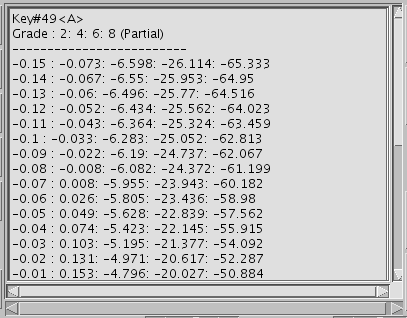
[ 49<A> 0.5 ]テキスト表示:
カーソル位置の[ キー名: データ ] を表示します。
データは [Inha.]ではインハーモニシティ値を
それ以外ではセント値を表示します。
[ Octave 2:1 ]セレクタ: [Beat][All][Grad.]で表示する音程を選択します。
[ 8 ]セレクタ: [Beat][All][Grad.]で表示する倍音数を選択します。(1〜20倍)
左側[ Inha(rmonicity) ]ボタン: インハーモニシティ値を表示します。
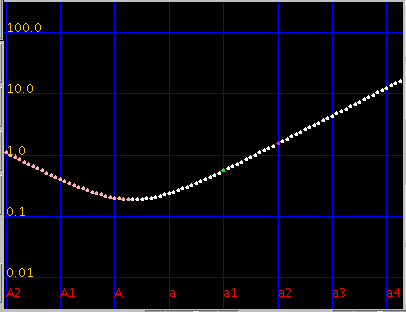
[ Cent ]ボタン:セント値を表示します。 (v0.4)インハーモニシティ値を加え無くしました。
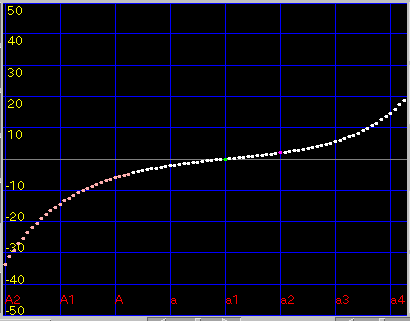
[ Beat ]ボタン: 現在のキーをセント値で変化させた時の`うなり'を表示します。
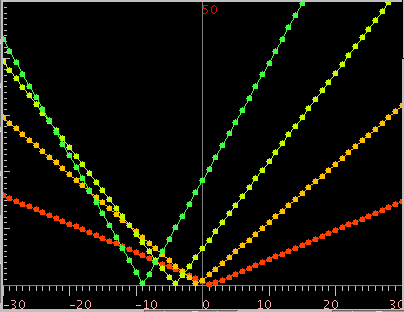
[ All ]ボタン: キー全体の`うなり'を表示します。
[ Grad(e) ]ボタン:
現在のキーで
傾き(grade)を-0.15から0.15に変化した時の`うなり'を表示します。
[Grad.]のスクロールバーの変化範囲は 0から0.15で
縦のカーソル線で示しています。

[ Text / Grap. ]トグルボタン: グラフ表示又はテキストデータ表示に切替えます。
右側[ + ][ - ]ボタン: 表示画面を上下に増減します。
[ < | > ]ボタン: [Beat]表示で左右の移動セント範囲を増減します。
下段[ Curve / Straight ]トグルボタン: インハーモニシティ値を[Curve](曲線) 又は[Straight](直線)に切替えます。
[ Grade: 0.087 ]スクロールバー:
インハーモニシティの傾き(grade)を変更します。(0〜0.15)
[Curve]と[Straight]で範囲の数値を同じにしました。
[ Inha.: 0.55 ]スクロールバー: A(49)のインハーモニシティ値を変更します。(0〜1.1)
[ Bass: 28 ]スクロールバー: 巻線の数を変更します。(0〜48)
[ Tune / Clear ]トグルボタン: Tuningのシミュレーションの実行 又は セント値をクリア(0)します。
[ Beat: 1.0 ]スクロールバー: [Tune]時の`うなり'数を変更します。(0〜3.0)
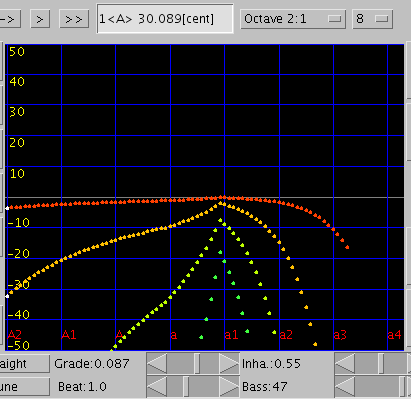
(v0.3)幾つかの[Grad.]を見てみます。 オクターブの A(1)とC(28)とA(61)です。(巻線数は27です。)
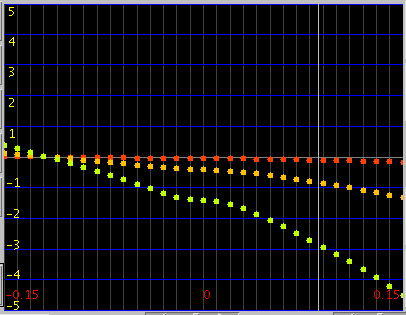
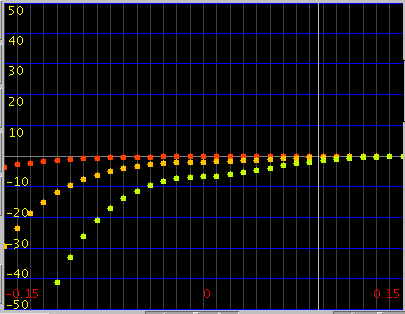
例えば巻線の数を0にしてみます。
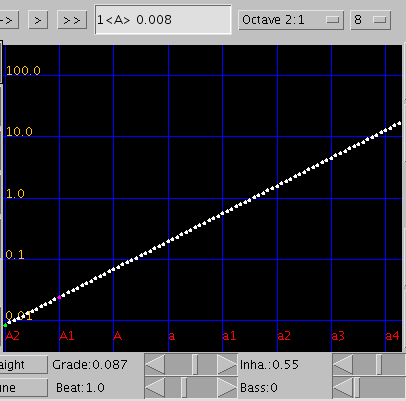
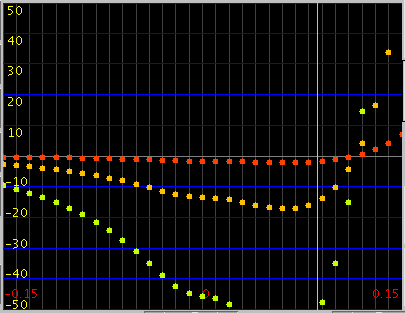
A(1)の傾き(Grade)を見てみます。
[Grad.]はマイナスで`うなり'が大きくなります。
右はその時の[Inha.]の変化と[All]の`うなり'です。
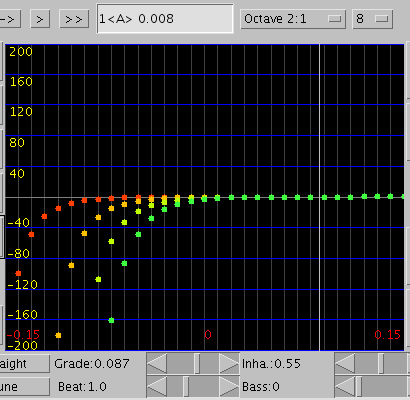
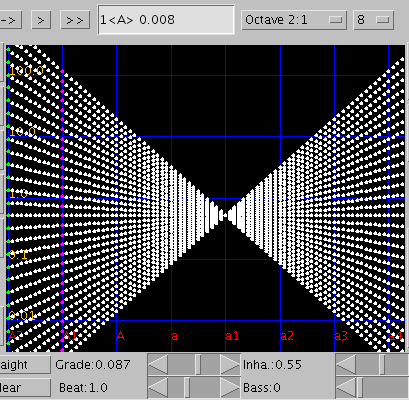
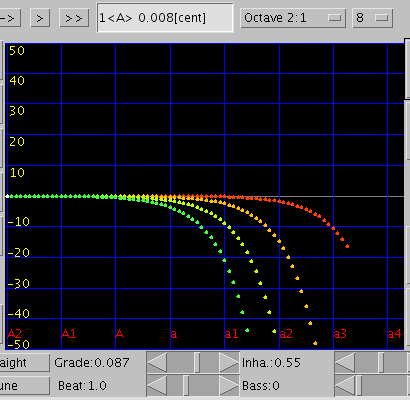
巻線の数を増やしてみます。
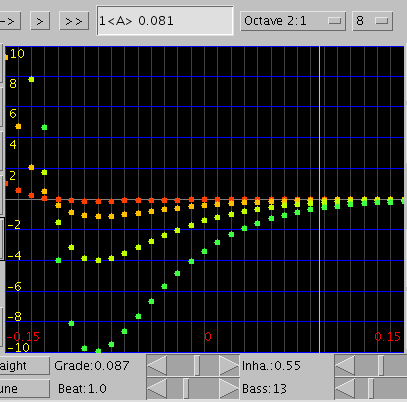
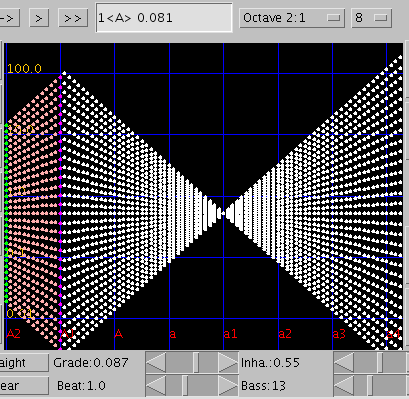
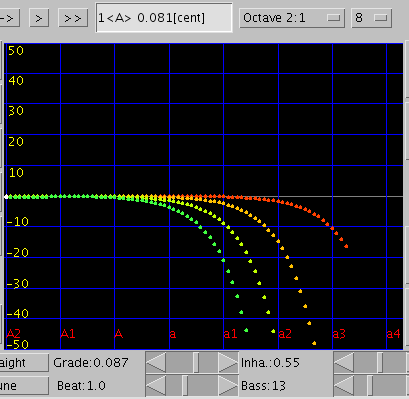
13本ではプラスと同じく -0.11~-0.12で`うなり'の逆転が起こり -0.087前後で`うなり'のピークがある事が見受けられます。
巻線27本の場合です。
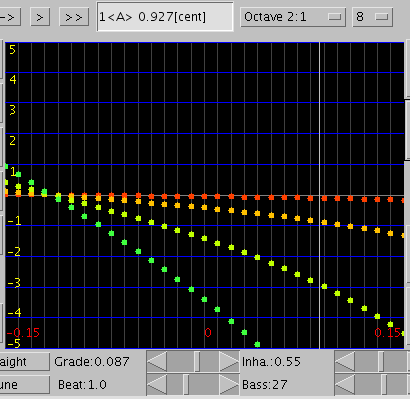
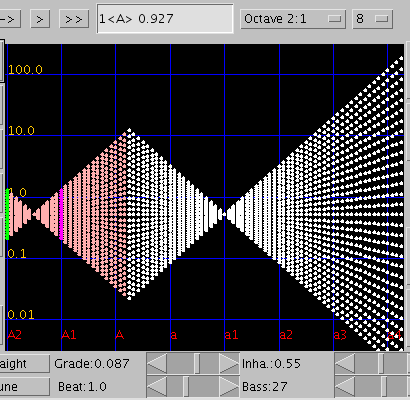
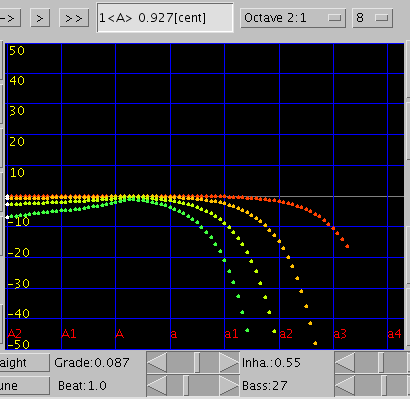
傾き(grade)の増減に比例して `うなり'が同じように増減するのが分かります。
巻線37本の場合です。以降は増加するのみです。
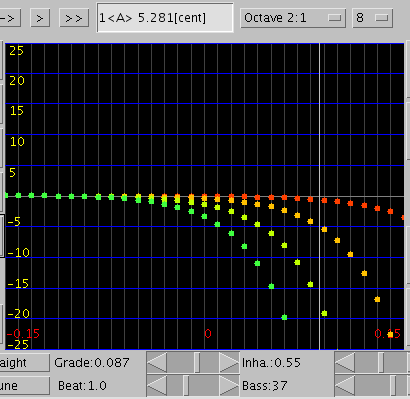
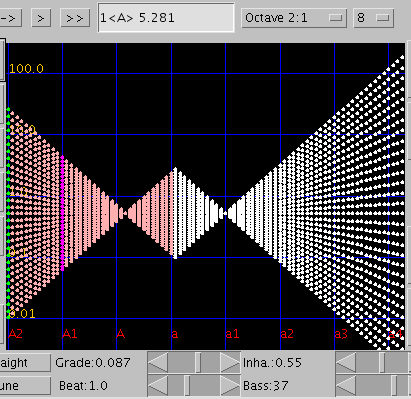
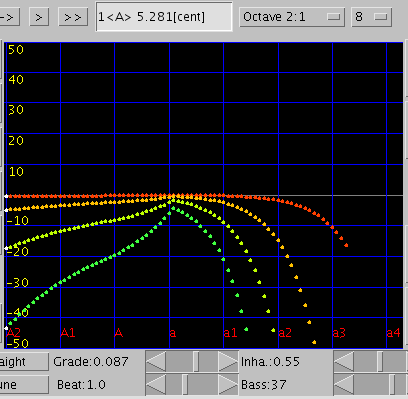
巻線47本の場合です。
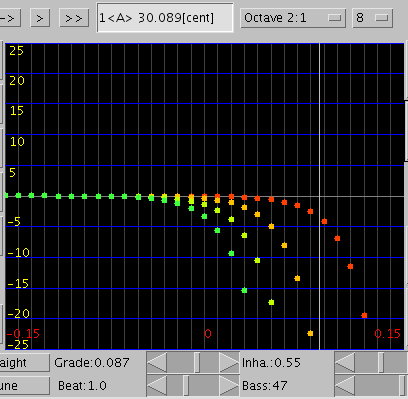
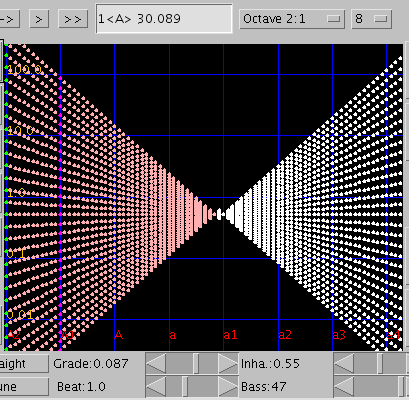
初めに平均律の場合 オクターブ(2:1)での倍音の`うなり'は
| Key\倍数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8... |
|---|---|---|---|---|---|---|---|---|
| A(37) | 220 | 440 | 660 | 880 | 1100 | 1320 | 1540 | 1760... |
| A(49) | 440 | 880 | 1320 | 1760 | 2200 | 2640 | 3080 | 3520... |
A(49) 440[Hz] - A(37) 220[Hz]x2 (440) = 0 のように
どのキーでも 0になります。
4度(4:3)では
| Key\倍数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8... |
|---|---|---|---|---|---|---|---|---|
| A(37) | 220 | 440 | 660 | 880 | 1100 | 1320 | 1540 | 1760... |
| D(42) | 293.665 | 587.330 | 880.995 | 1174.660 | 1468.325 | 1761.990 | 2055.655 | 2349.320... |
D(42) 293.665[Hz]x3 (880.995) - A(37) 220[Hz]x4 (880) = 0.995 のように 1オクターブ高くなる毎に差は 2倍になります。
5度(3:2)では
| Key\倍数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8... |
|---|---|---|---|---|---|---|---|---|
| A(37) | 220 | 440 | 660 | 880 | 1100 | 1320 | 1540 | 1760... |
| E(44) | 329.628 | 659.256 | 988.884 | 1318.512 | 1648.140 | 1977.768 | 2307.396 | 2637.024... |
E(44) 329.628[Hz]x2 (659.256) - A(37) 220[Hz]x3 (660) = -0.744 のように 1オクターブ高くなる毎に差は 1/2倍になります。
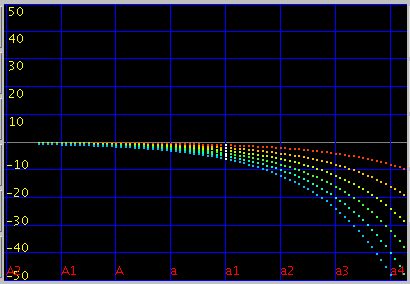
では 直線のインハーモニシティ 0.55・傾き(grade) 2.8(0.087)・セント値は全て 0[cent]で 未tuningの場合です。
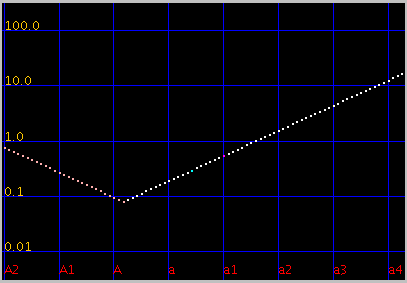
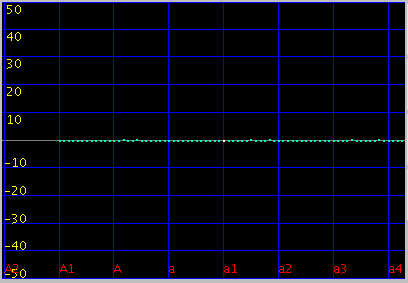
オクターブ・4度・5度の`うなり'は
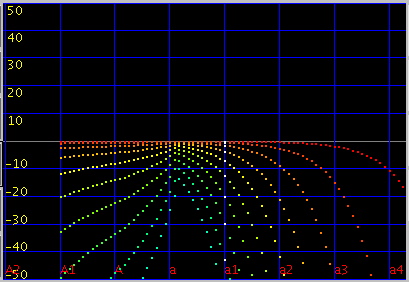
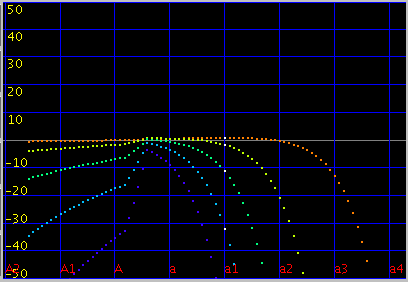
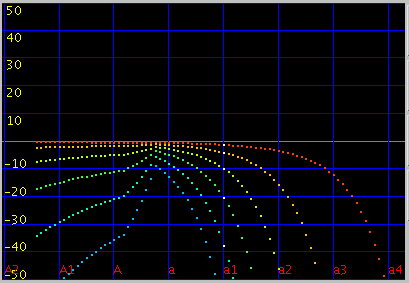
傾きを 1.9(0.055)にしてみます。
オクターブ・4度・5度の`うなり'は
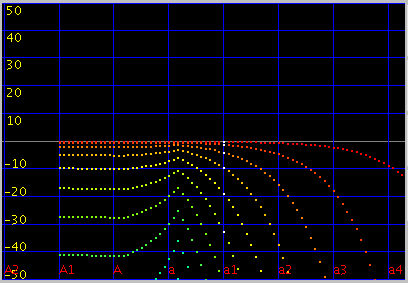
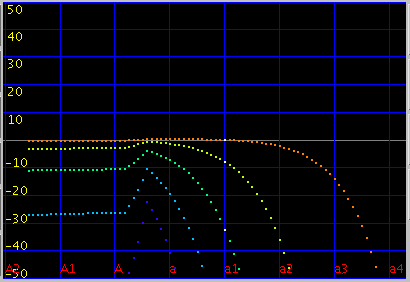
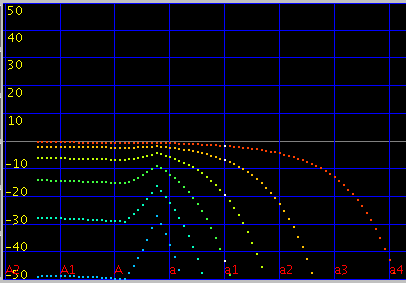
傾きを 4.2(0.12)にしてみます。
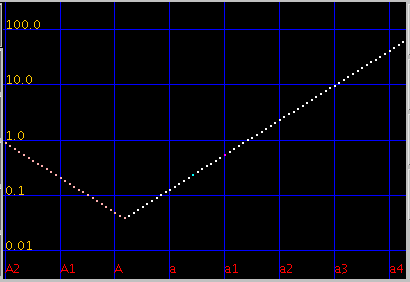
オクターブ・4度・5度の`うなり'は
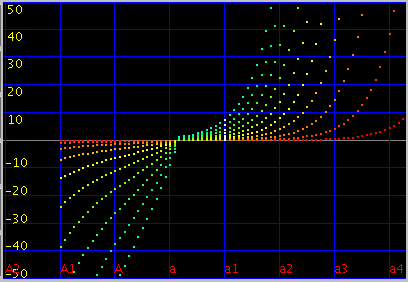
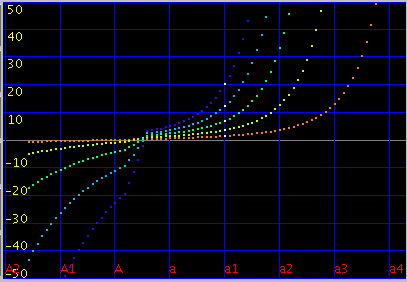
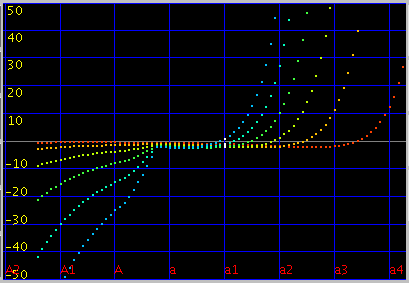
次に 曲線のインハーモニシティ 0.55で 傾き(grade) 0.087の場合です。
オクターブ・4度・5度の`うなり'は
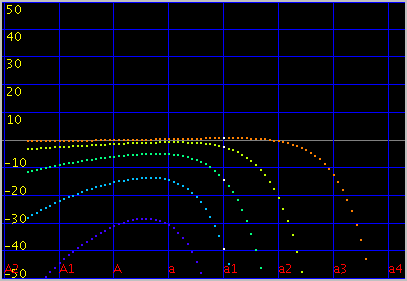
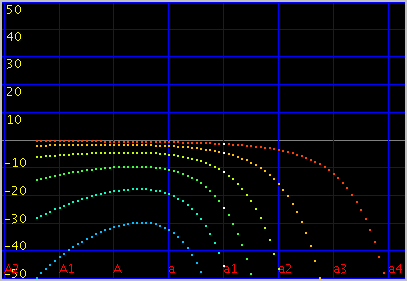
傾き(grade)を 0.065にします。
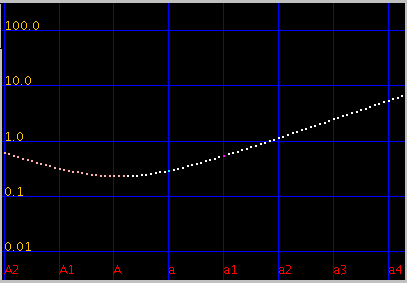
オクターブ・4度・5度の`うなり'は
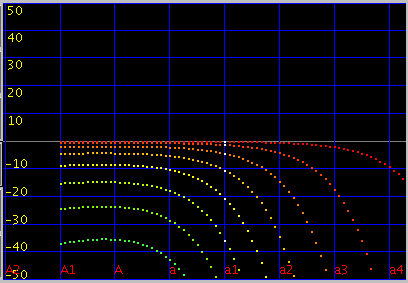
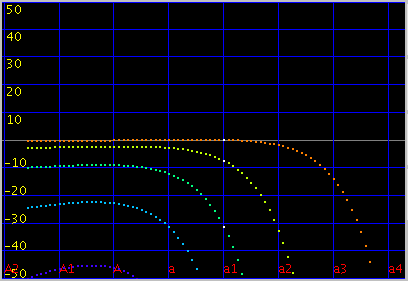
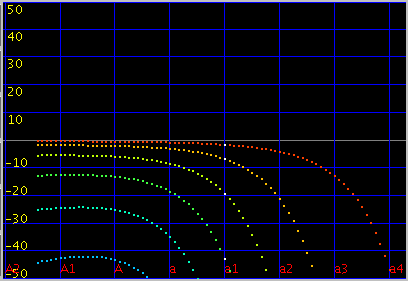
傾き(grade)を 0.117にします。
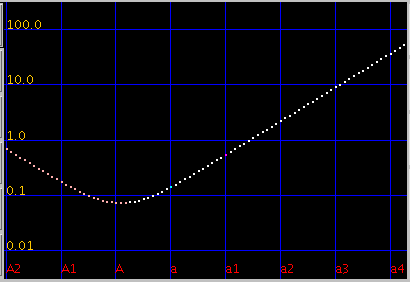
オクターブ・4度・5度の`うなり'は
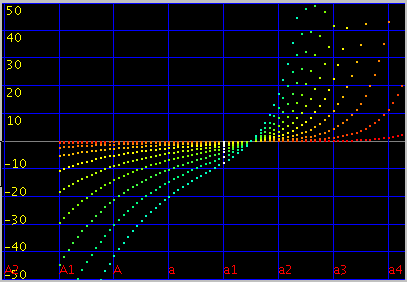
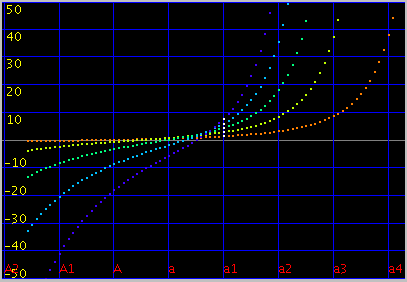
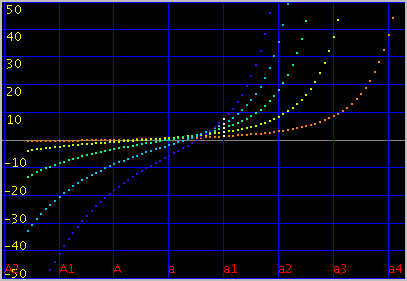
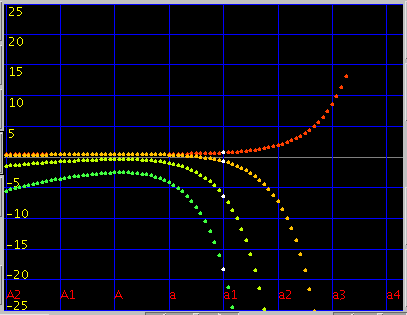
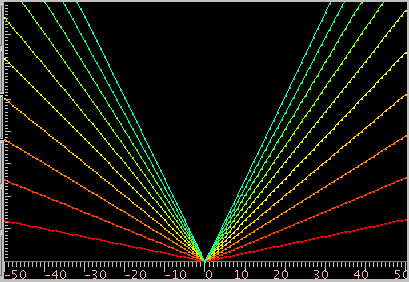
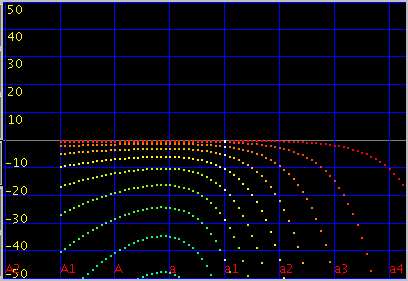
曲線の傾き(grade)を -0.15〜0.15で変化させてみます。
キー毎の`うなり'で A(1)キーです。 (以後全て 3倍音まででみます)
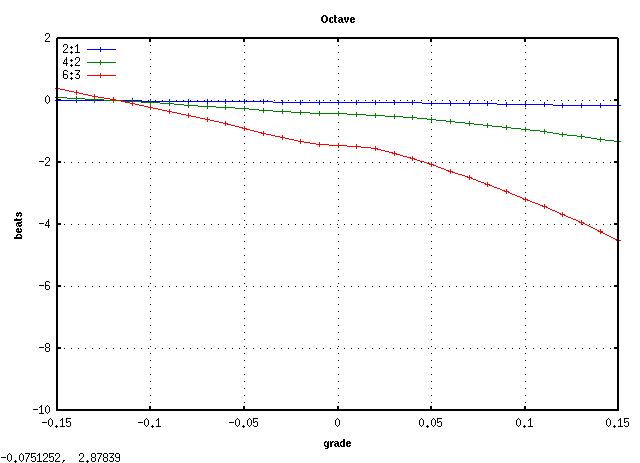
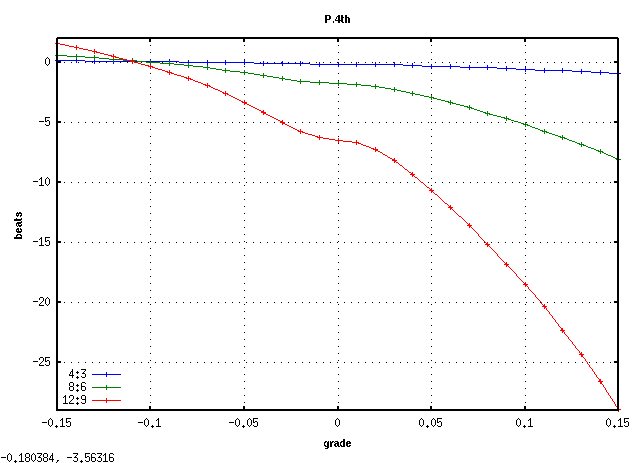
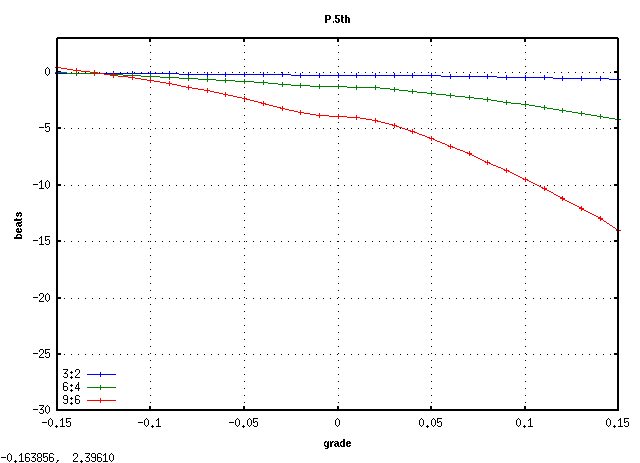
A(1)キーから 3キー毎に C(28)キーまでです。
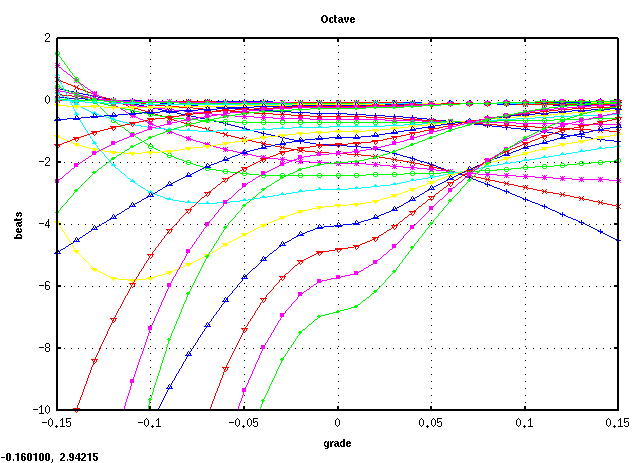
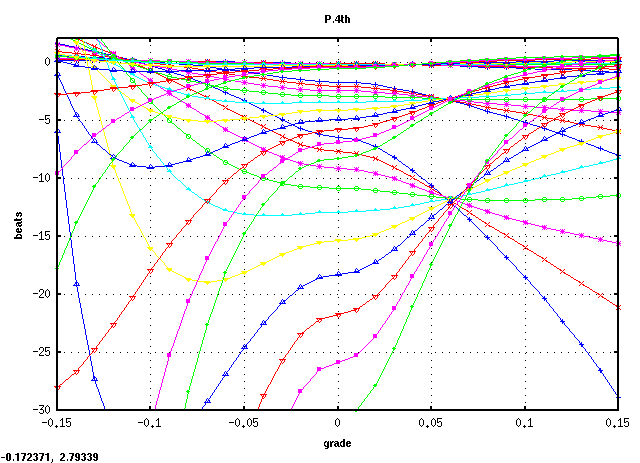
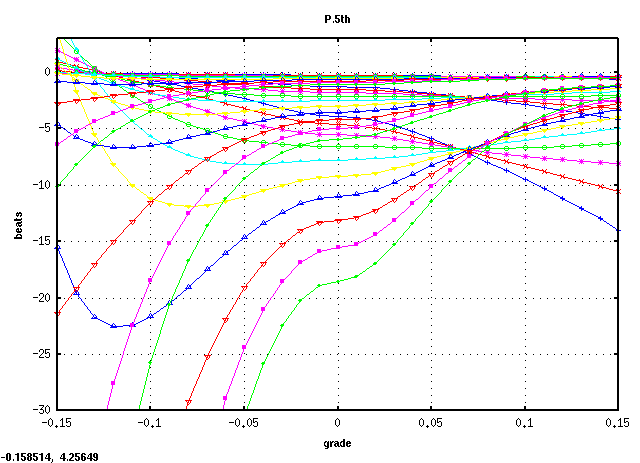
C(28)キーです。
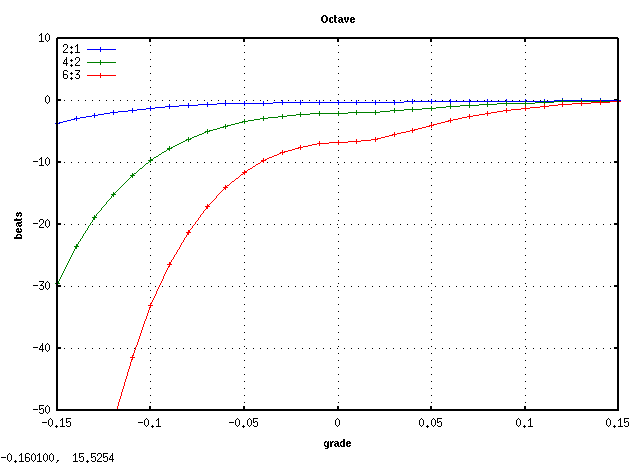
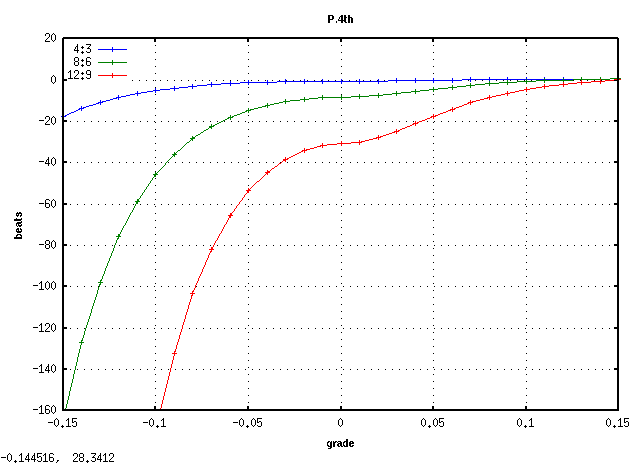
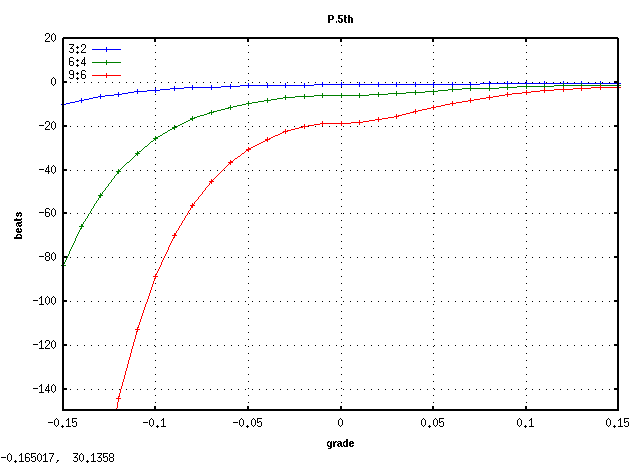
C(28)キーから 3キー毎に A(61)キーまでです。
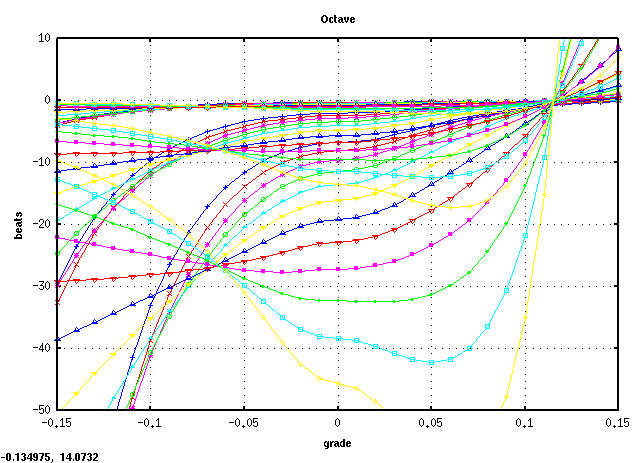
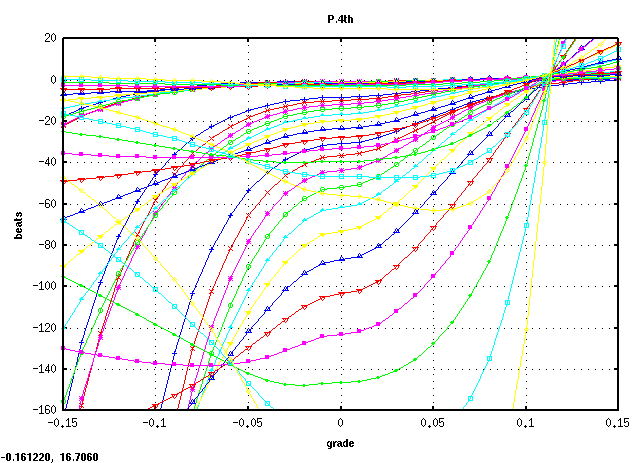
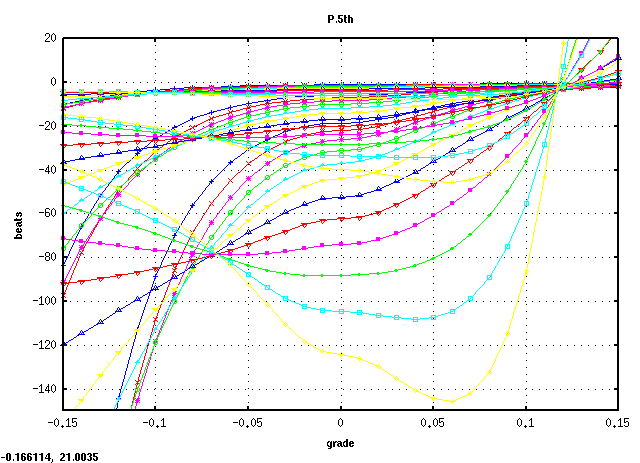
A(61)キーです。
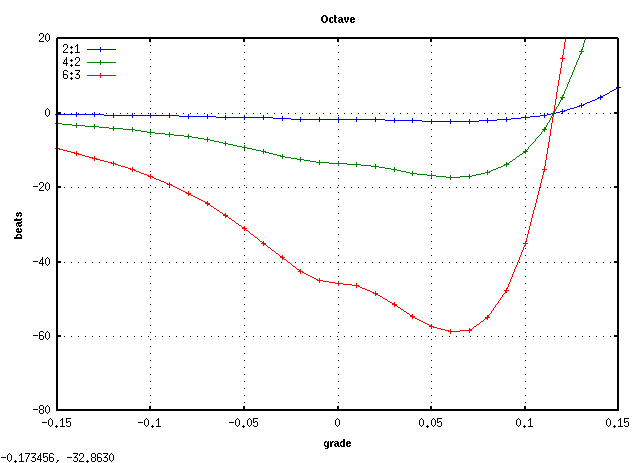
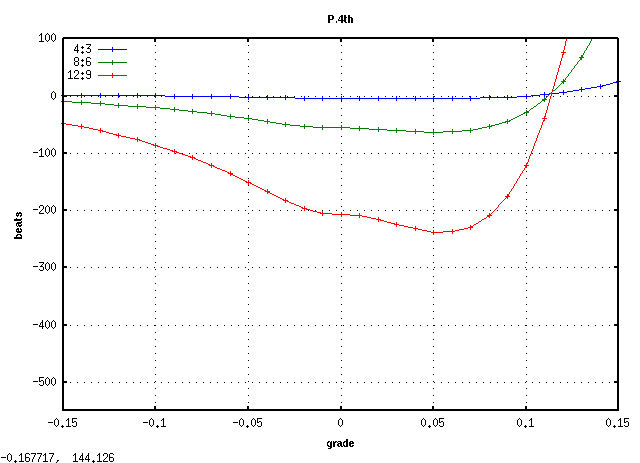
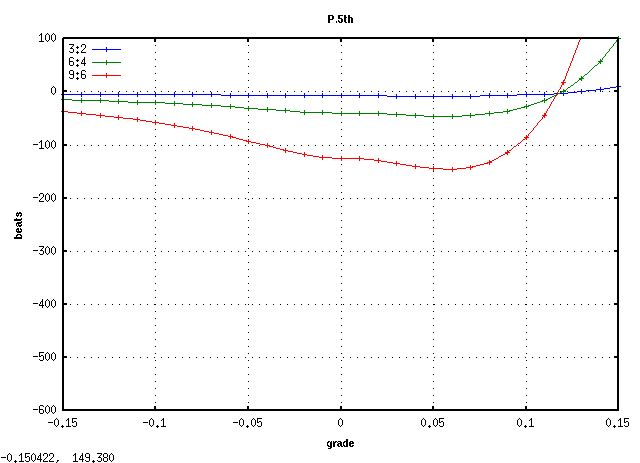
A(61)キーから 3キー毎に C(88)キーまでです。
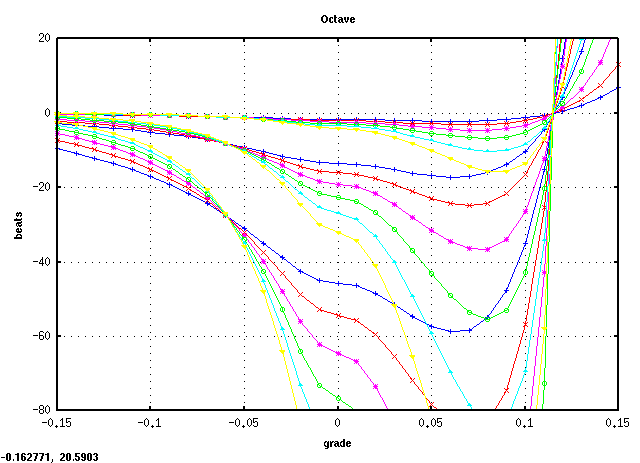
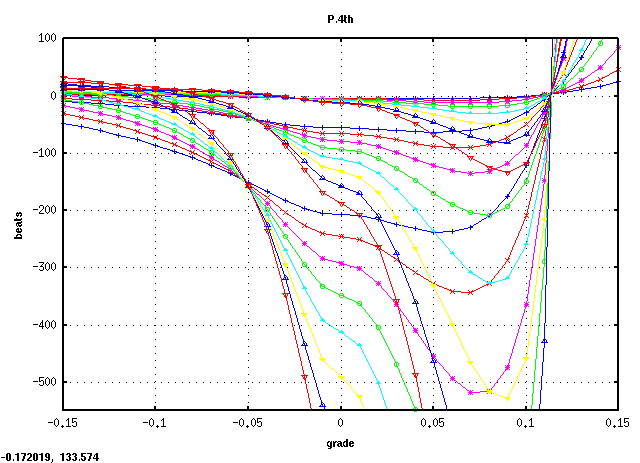
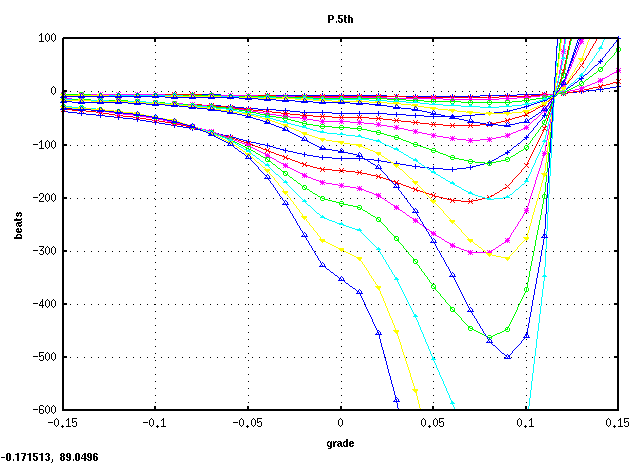
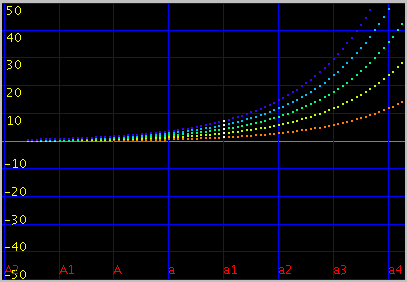
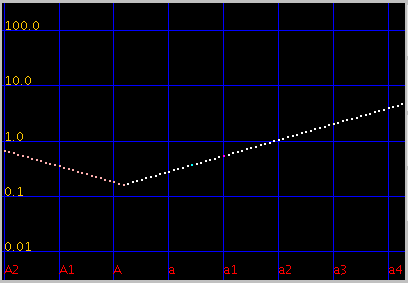
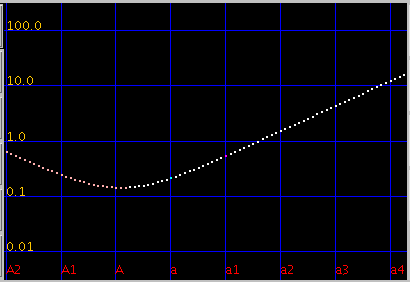
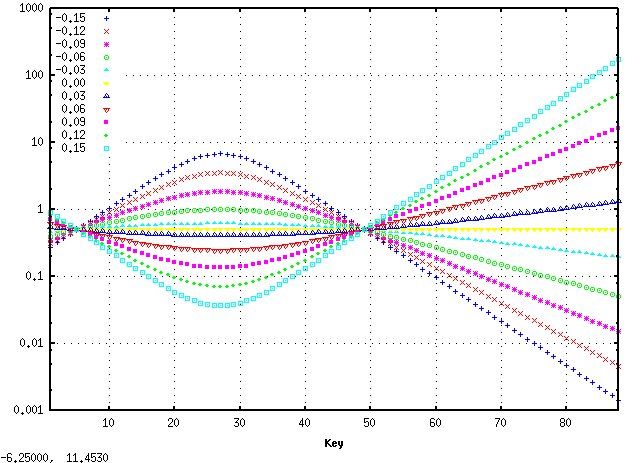
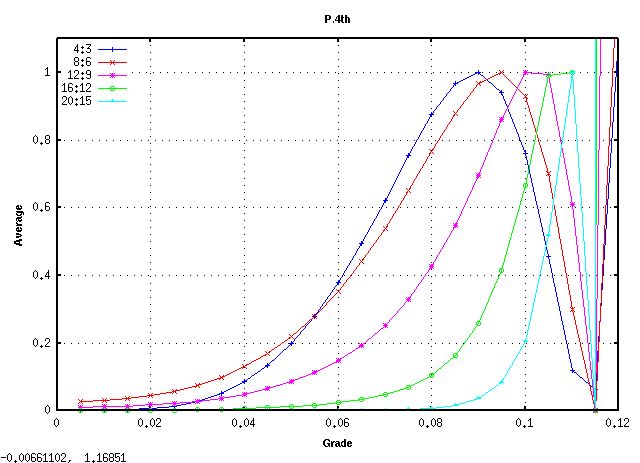
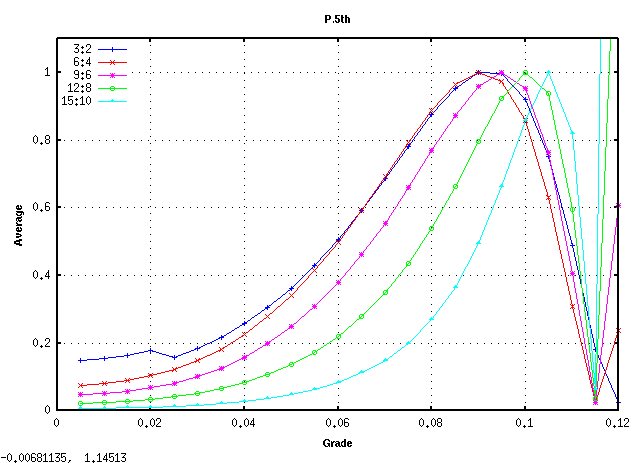
全てのキーの`うなり'の広さ (全ての`うなり'の合計をキー数で割った平均値)は 見安くするために高さを揃えています)を見てみます。
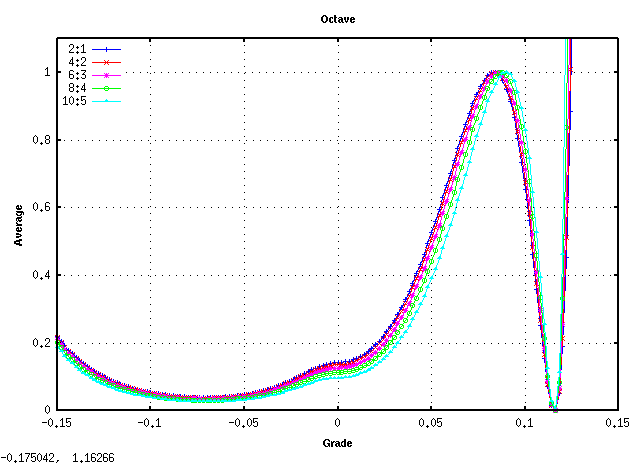
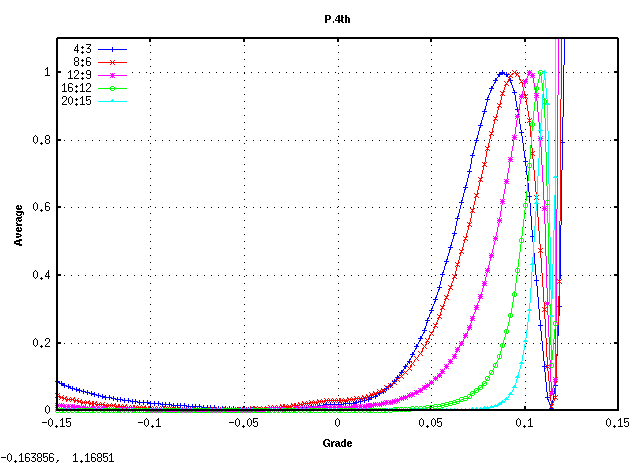
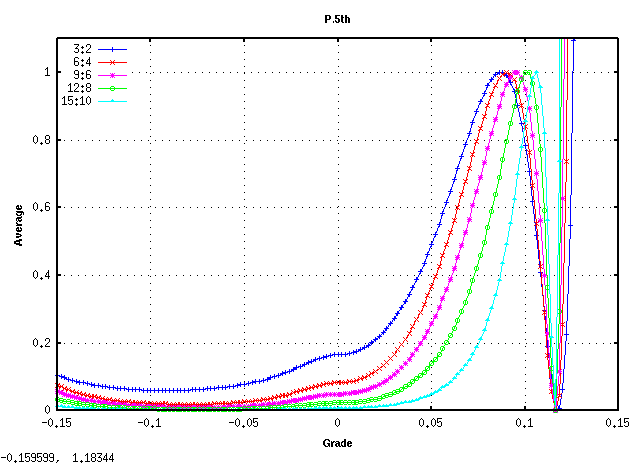
平均的にオクターブで 倍音が最も広くなるのは
傾き(grade) 0.08~0.09ぐらいになります。
また 0.115前後で平均律の様な`うなり'が 0となる地点があり
それ以上では反転します。
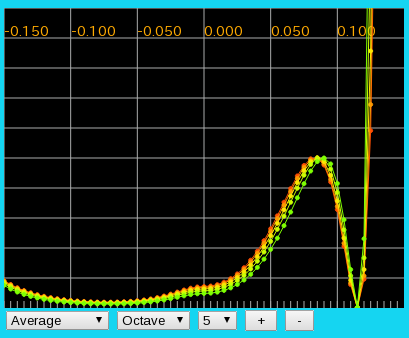
HTML5版です。
Tuning(のシュミレーション)を行うと 多少変わります。 (左からオクターブ・4度・5度の`うなり'です)
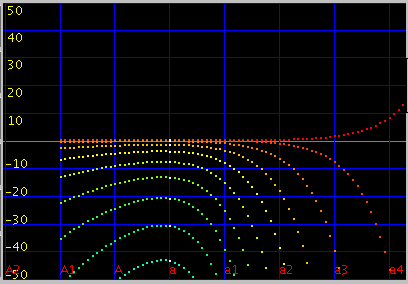
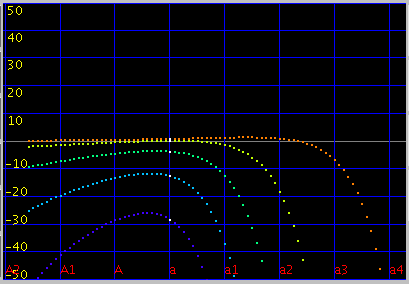
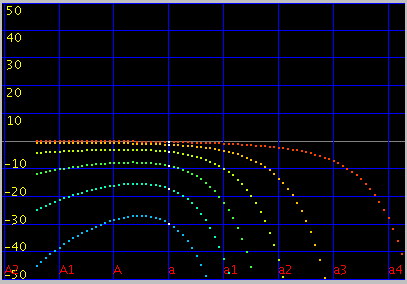
その場合の全てのキーの`うなり'の広さです。 (Tuningのシュミレーションの範囲は前より狭くなっています)
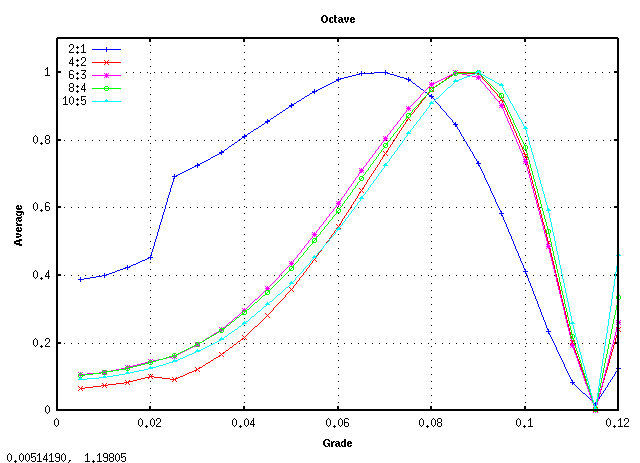
ところで インハーモニシティによる‘うなり’(Ibeats) では「Broadwood」の [Beat]が 高音部で逆転しています。
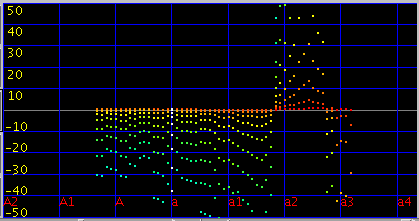
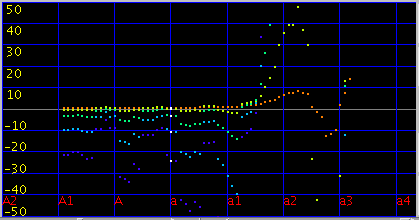
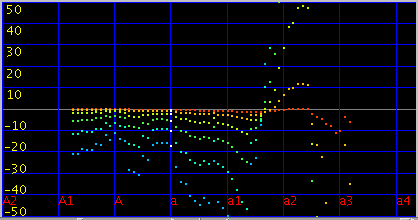
そのインハーモニシティ値を曲線(curve)で合わせた値です。
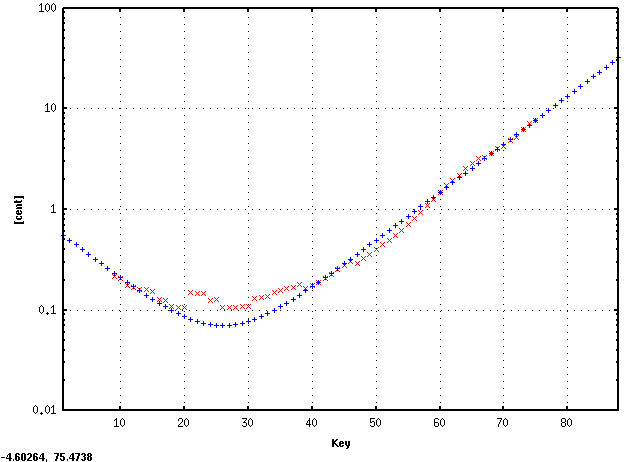
傾き(grade)[0.11]と 0.115に近い値となっています。 そして [design]のイマジナリーピアノでは
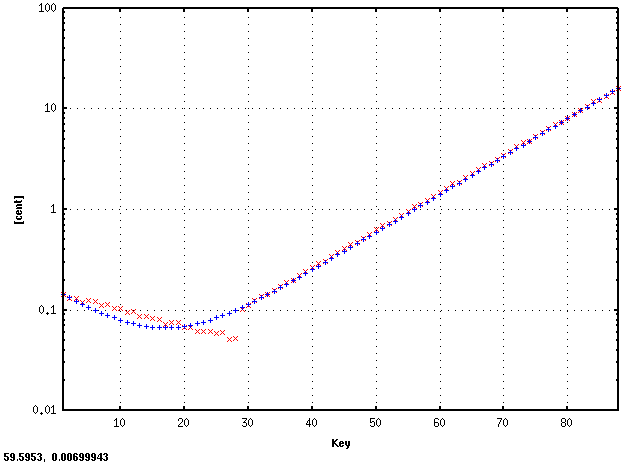
傾き(grade)[0.087] となります。
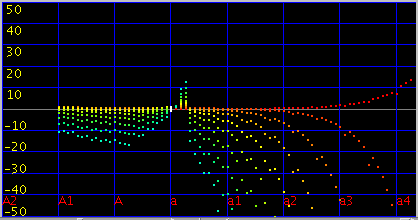
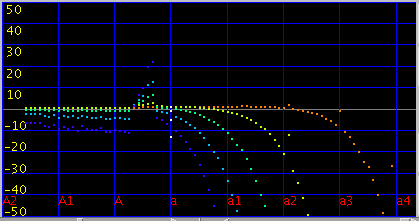
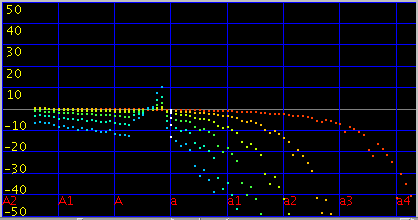
インハーモニシティの段差がある所では `うなり'の逆転が見受けられます。