第6回 Key Beats (平均律) #6

( 変更履歴:
v0.2 [11/10/30] ctofの計算式を変更しました。)

平均律の場合です。
2キー間で 片方のキーを変化させた時の 倍音の“うなり”の変化を見てみます。

function dispKbeats(key,inte)
  multiple = 1:5;   # 倍音の範囲
  widec = 15;       # ±セント値の範囲
  ratio = Interval(inte);
  for m = multiple
    ra = [ratio(1:2)*m inte];
    be = abs(getKbeat(key, ra, -widec:widec));
    plot(-widec:widec, be, '-@')
    hold on
  end
  hold off
  xlabel('[cent]')
  ylabel('Beat')
end

getKbeat.m はキー番号(37)の 間隔 5(4度)の 4:3の“うなり”を -5[cent]から 5[cent]までの 1[cent]間隔で求めます。

> getKbeat(37, [4 3 5], -5:5)
ans =

 Columns 1 through 7:

  -1.546437  -1.038876  -0.531021  -0.022873   0.485568   0.994304   1.503333

 Columns 8 through 11:

   2.012656   2.522274   3.032186   3.542393

function beat = getKbeat(key,ratio,cent)
  freq1 = getFrequ(key) * ratio(1);
  freq2 = getFrequ(key + ratio(3)) * ratio(2);
  freq2 = ctof(freq2, cent);
  beat = freq2-freq1;
end

ctof.m は セント値から周波数を求めます。

> ctof(220, 1200)
ans =  440

220[Hz]の +1200[cent]は 1オクターブ上の 440[Hz]になります。

function f = ctof(freq, cent)
  f = freq.*2.^(cent/1200);
end

上記の様に 3つのファイルに分けます。
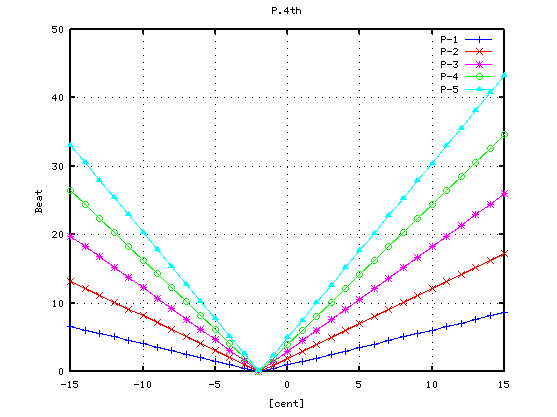
キー番号(37)のキー間隔 5(4度)の 倍音の“うなり”の変化をみます。

> dispKbeats(37, 5)

さらに 画面に説明を加えます。

function dispKbeats1(key,inte)
  multiple = 1:5;   # 倍音の範囲
  widec = 15;       # ±セント値の範囲
  [ratio rstr]= Interval(inte);
  for m = multiple
    ra = [ratio(2:3)*m inte];
    be = abs(getKbeat(key, ra, -widec:widec));
    str = strcat(';P-', num2str(m), ';-@', getCP(m));
    plot(-widec:widec, be, str)
    hold on
  end
  hold off
  title(rstr)
  xlabel('[cent]')
  ylabel('Beat')
  grid on
end

-------ここまで-------

> dispKbeats1(37, 5)