 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
その1:
例えば「ある音から 1[Hz]づつ変化して行く音との間に
どんな‘うなり’が生じるのでしょう?」
周波数発振器ではサインカーブで倍音は出ないし矩形波では聞くに耐えないし…
でシミュレーションしてみました。
(ボタンを押して下さい。別のフレームで Javaが実行されます。
S・M・LでJava画面のサイズを選べます)
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
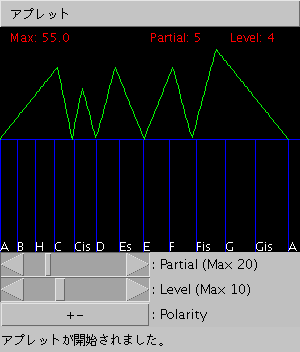
画面は横軸が1オクターブ分の周波数で縦軸は‘うなり’の数です。
「A(37) 220Hz」の音に対して1Hzずつ 1オクターブ上まで増加して行く 音の‘うなり’の数を緑のラインが表します。 (2倍音の図で分かる通り,下の Aが220[Hz]の時に最大で110回となります)
「倍音数」(Partial)スライダーを可変することで倍音成分が増減します。
「絶対値」(Absolute Value)ボタンで‘うなり’の数を ±値または絶対値で表示するよう切替えます。
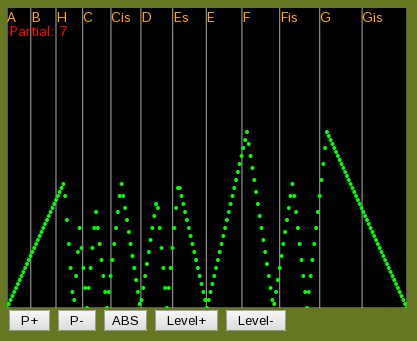
HTML5版です。
ビートについて FFTの視点を採り入れて見ました。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
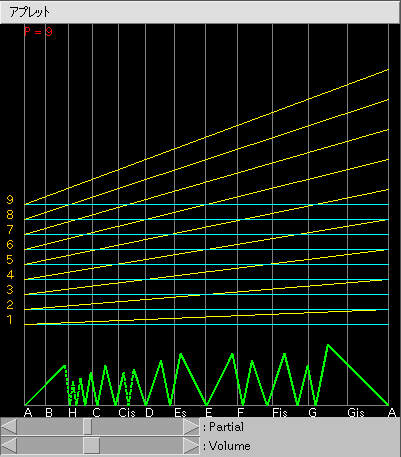
Javaの画面は 2つの図表を表しています。
シアン色のラインから上は「FFT画面」です。
縦軸は周波数です。
上に行く程高くなる対数表示になっています。
そのシアン色のラインは
ある周波数の基音とその倍音です。
黄色のラインは ある周波数の基音からその 2倍音(1オクターブ上)まで スムースに変化して行く音と その倍音です。
そして 横軸はオクターブまでに経過する時間で 左から右へと変化して行きます。
下段は「うなり画面」で緑色のラインは ある一定の周波数の音と その音から1オクターブ上まで増加する2つの周波数間の ‘うなり’の数を表します。 (縦軸が‘うなり’の数・横軸は左端から始まって右端が1オクターブ上です)
その周波数が1倍音(Partial)のみの時は‘うなり’は
その周波数の差そのままです。
オクターブになるまでうなりは増加し続けて行きます。
2倍音がある場合はオクターブに近ずくに従って ‘うなり’が 0に近付きます。
3倍音がある場合は,変化しないシアン色の3倍音と 変化する黄色の2倍音が1点で交差し ‘うなり’0の地点となります。
それが 純正5度の共鳴周波数(2 : 3)です。
4倍音まである場合では,それに純正4度(3 : 4)の‘うなり’0
の地点が加わります。
(注:6倍音の時,交差点が 6箇所あるのに‘うなり’0の地点が両端を除いて
5箇所なのは 2 : 3と 4 : 6が同じ5度の地点で重なっているからです)
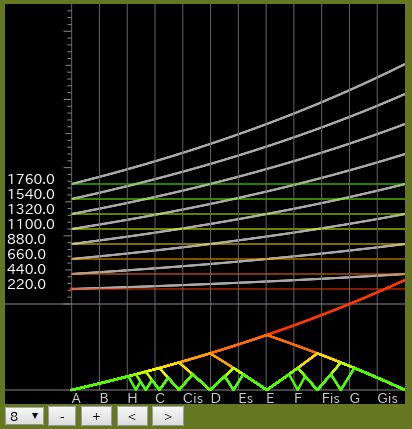
HTML5版です。
その3: インハーモニシティによる‘うなり’
その4: インハーモニシティの‘うなり’をスペクトログラムで見る
その5: FFTで見る`うなり'
その6: ビートへのまなざし