HTML5版です。

HTML5版です。
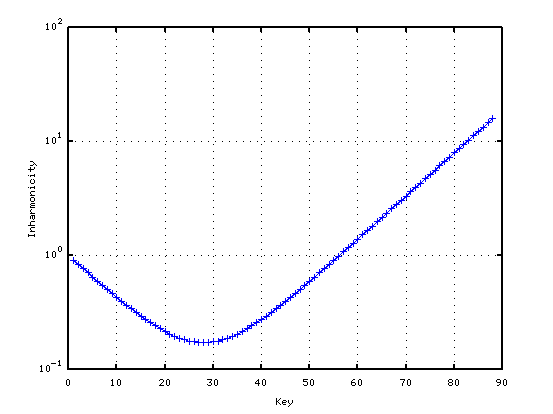
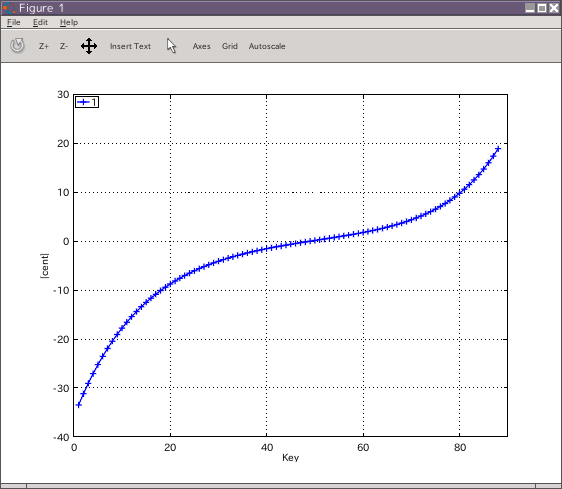
曲線の傾き(Grade) 0.087で A49のインハーモニシティ値を 0.55
のピアノをシミュレーションして
さらに Tuningのシミュレーション(2オクターブの`うなり'を 0)を行います。
そのインハーモニシティ値とセント値です。
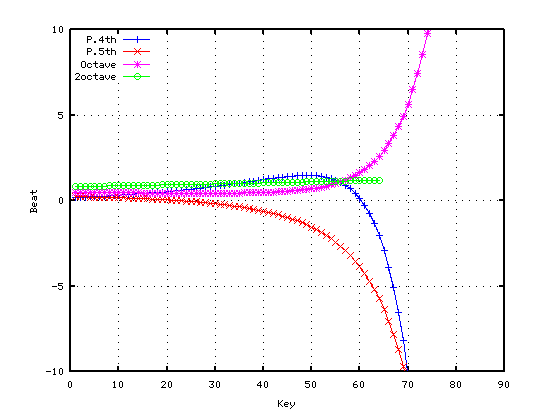
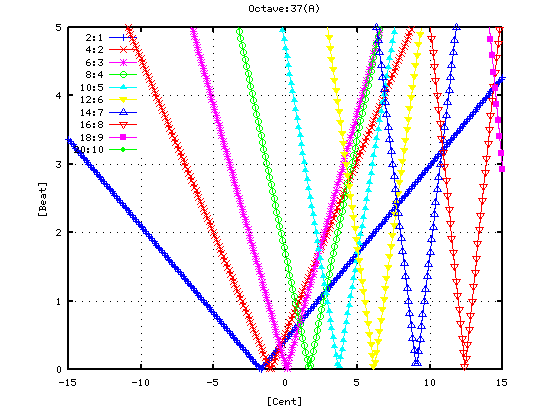
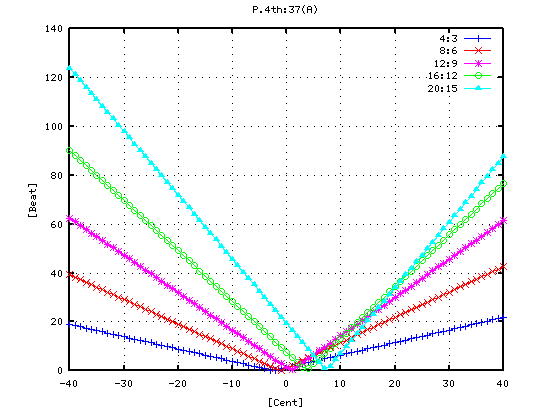
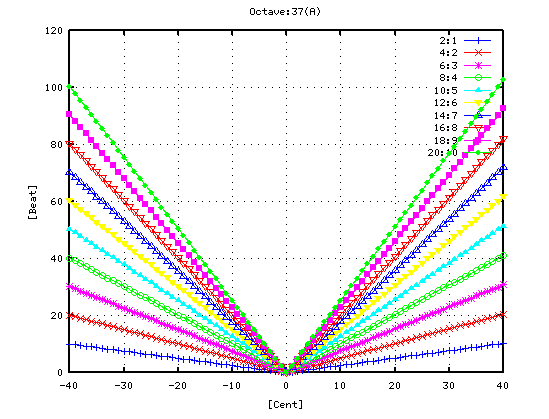
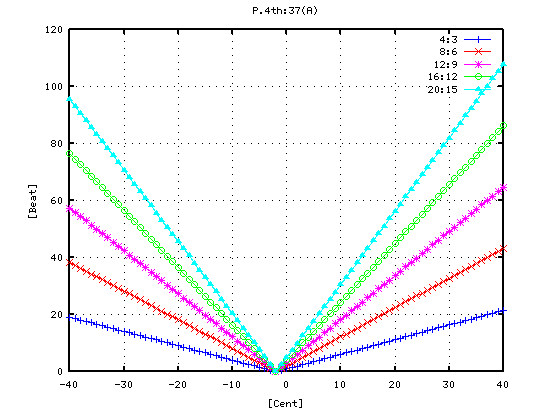
その時の 4度・5度・オクターブ・2オクターブの`うなり'は 以下の様になります。
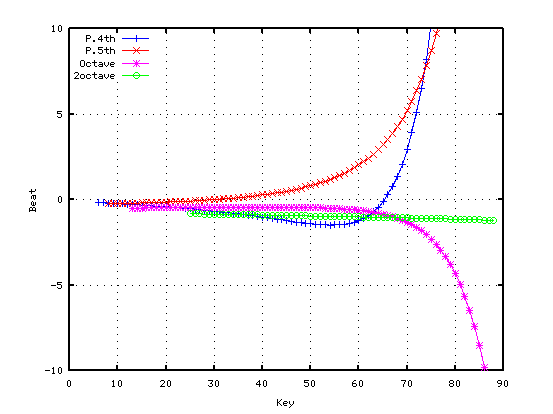
さらに 逆方向(例えば A37からA25へのオクターブの様に)に採ると `うなり'は以下の様になります。
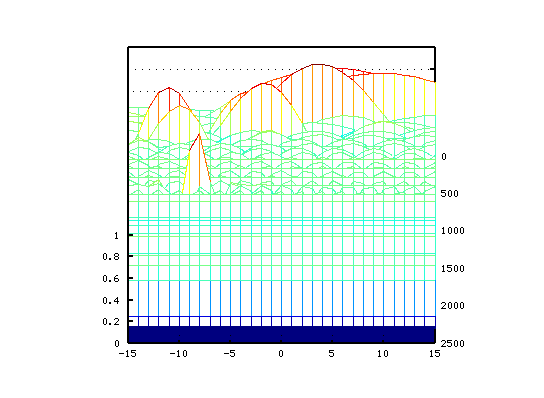
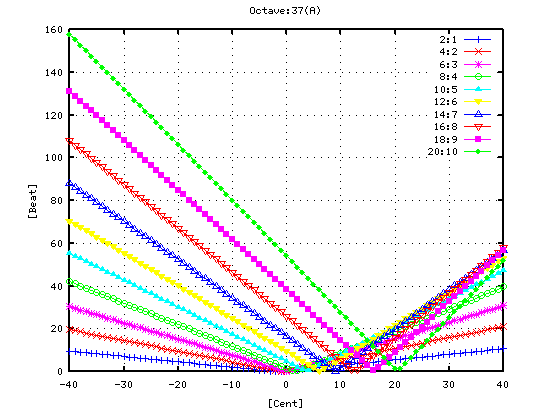
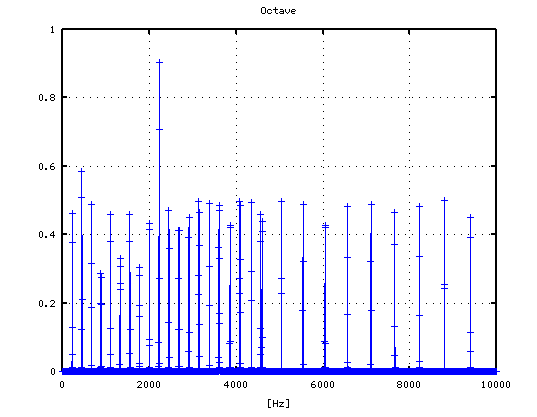
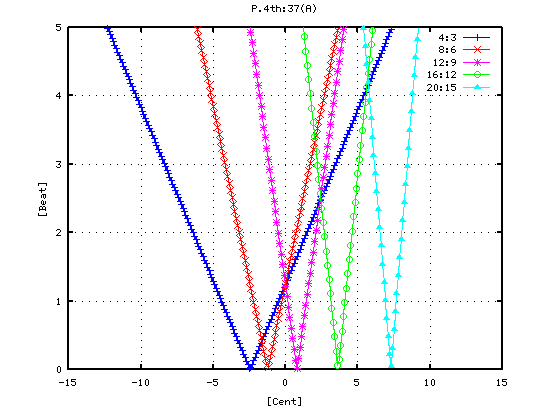
その時の オクターブ(A37-A49)の`うなり'の数を見てみます。 (右は 0[cent]を中心に拡大したものです。)
参照〉 ピアノのための初級Octaveプログラミング講座 (Octave) /第8回 Key Beats (Inharmonicity)
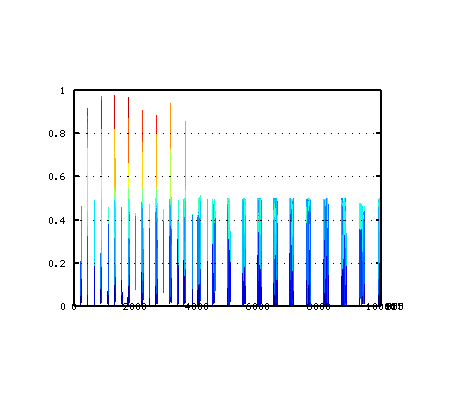
それを -3から +4[cent]まで 1[cent]ずつ変化させた Wave信号によるFFTのスペクトルで見てみます。
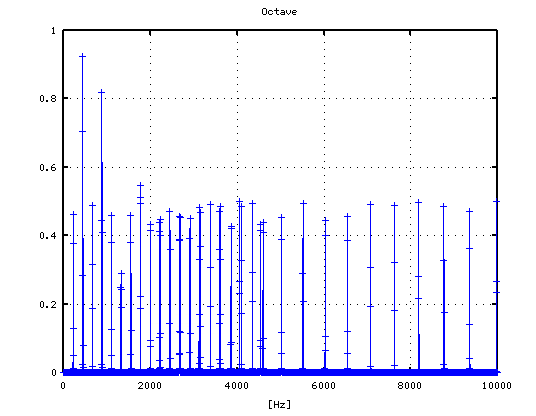 -3
-3
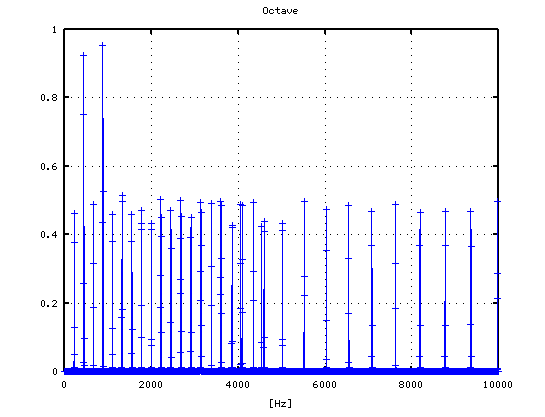 -2
-2
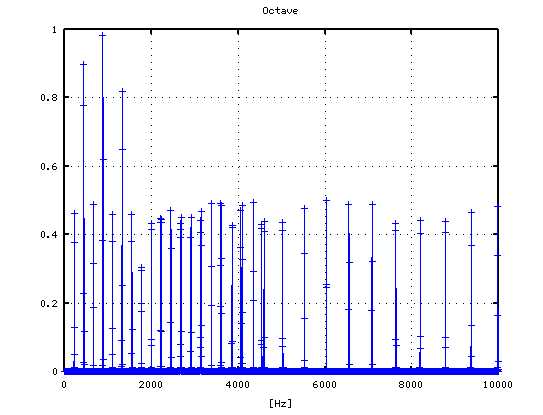 -1
-1
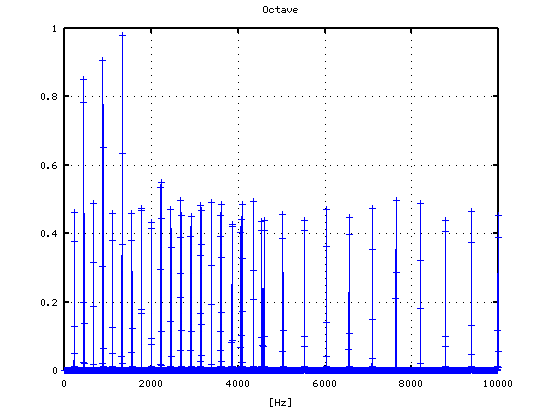 0
0
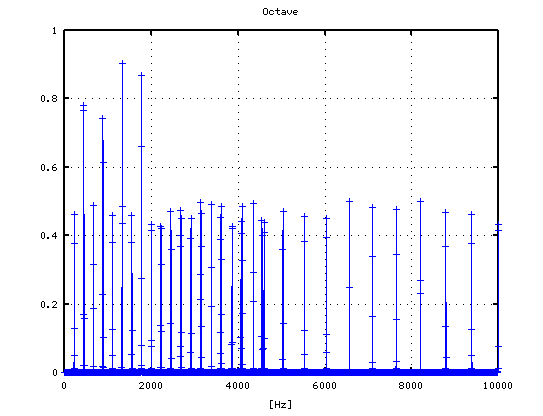 1
1
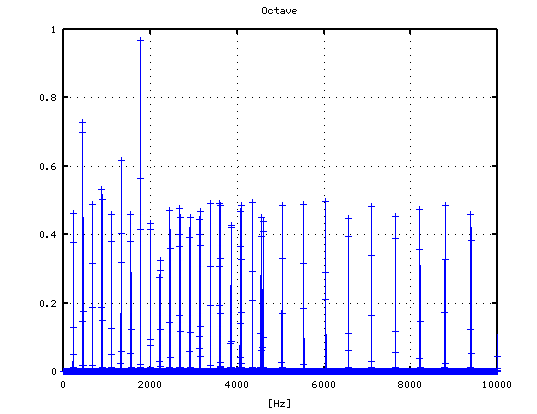 2
2
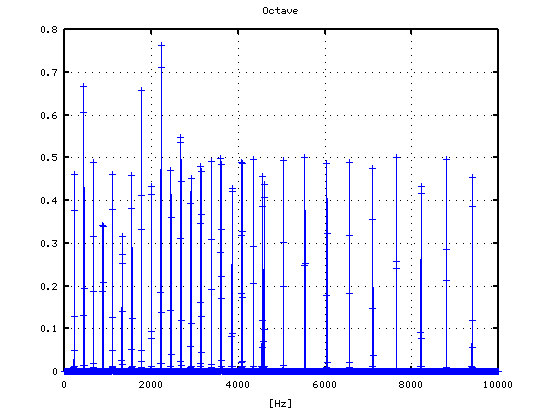 3
3
 4
4
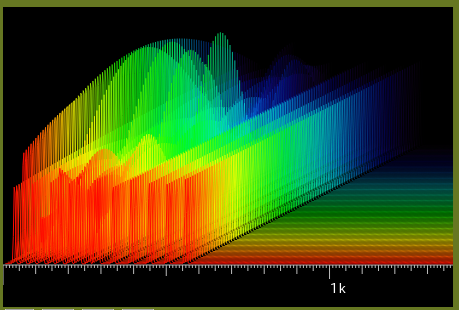
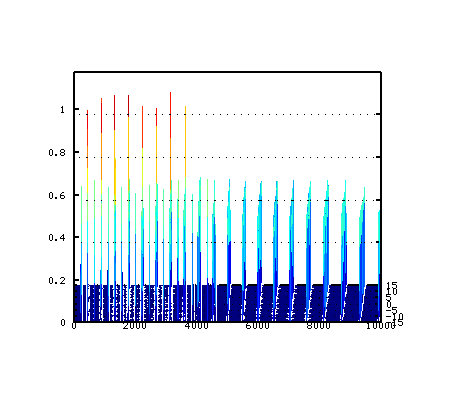
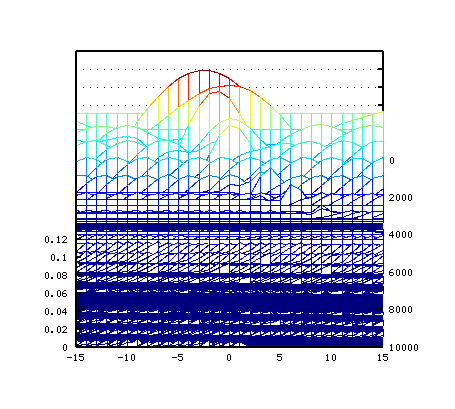
そのスペクトルを順に並べて 立体(3D)的にして見てみます。
少しずつ角度を変えて行きます。
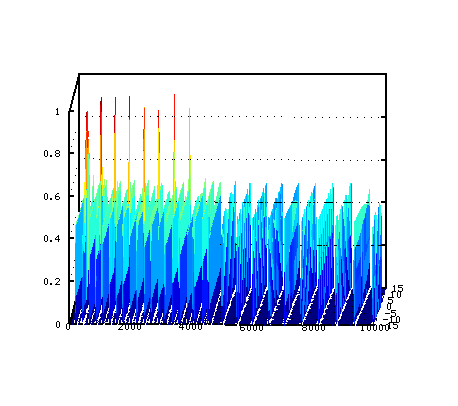
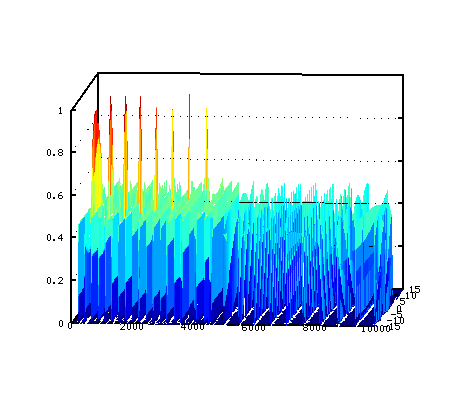
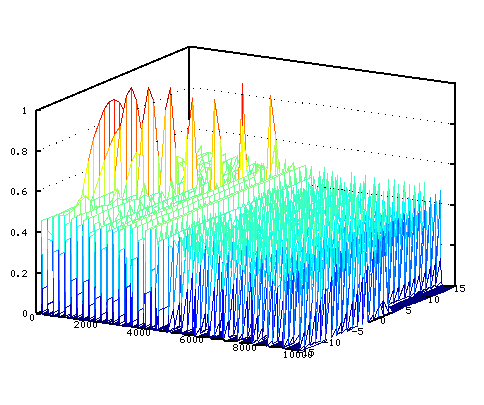
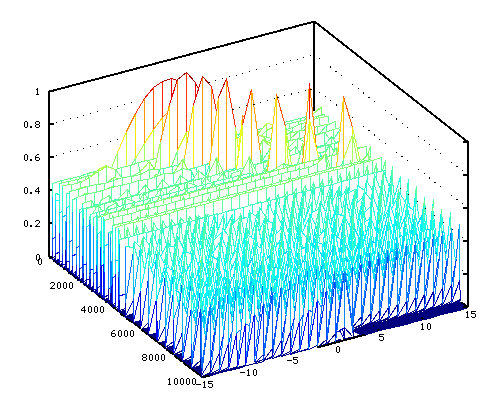
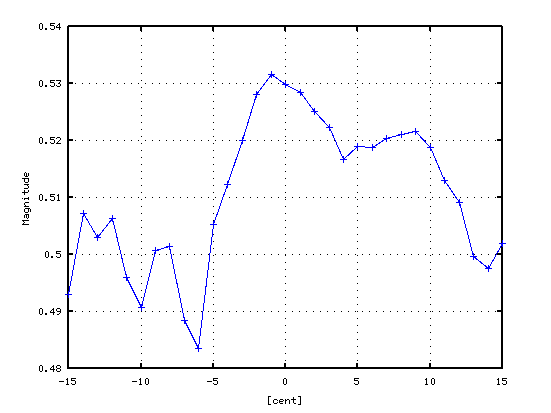
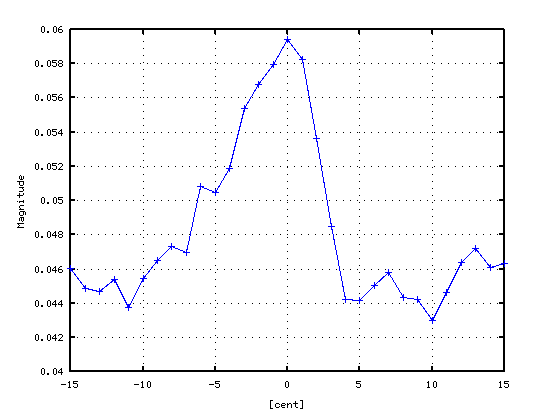
そして セント値を横軸にした方向から見てみます。 それと ピークの平均値をグラフにして見ます。
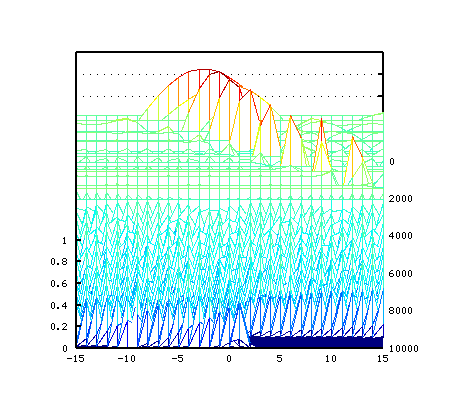
オクターブは 2:1の倍音が合うのは -3[cent]ぐらいですが
A49キーを 少し高く(広く)しています。
2:1の倍音のスペクトルが最も高い点よりも
4:2・6:3などの倍音も高くなる事で 音量が豊かになっていますが
それは ピークの平均値でも見てとれます。
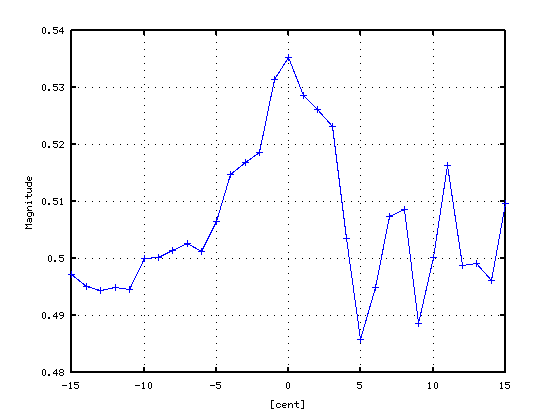
4度(A37-D42)の場合です。
そして -4から +3[cent]まで 1[cent]ずつ変化させた FFTのスペクトルを見てみます。
 -4
-4
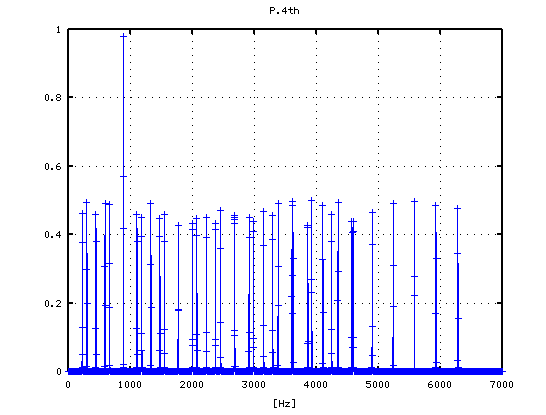 -3
-3
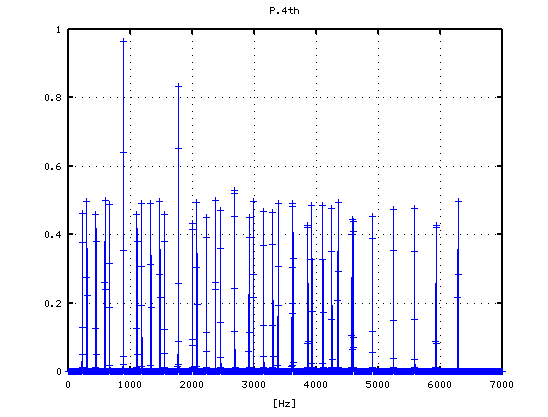 -2
-2
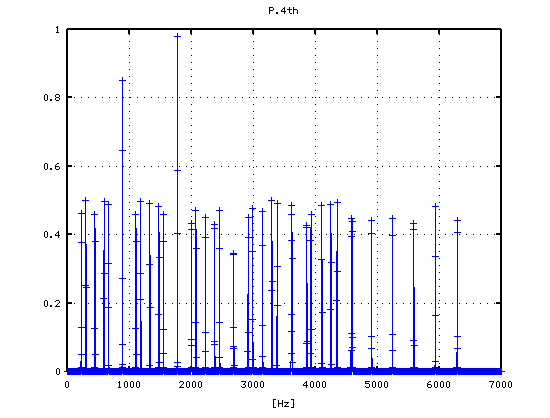 -1
-1
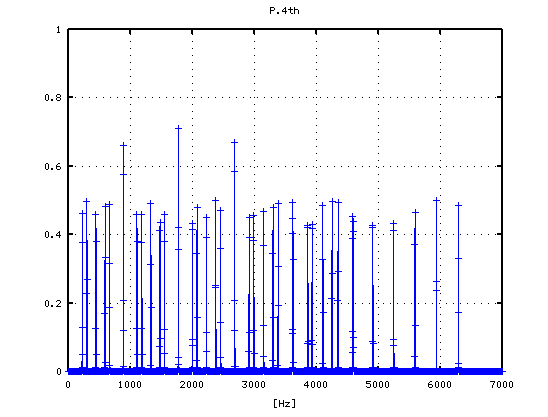 0
0
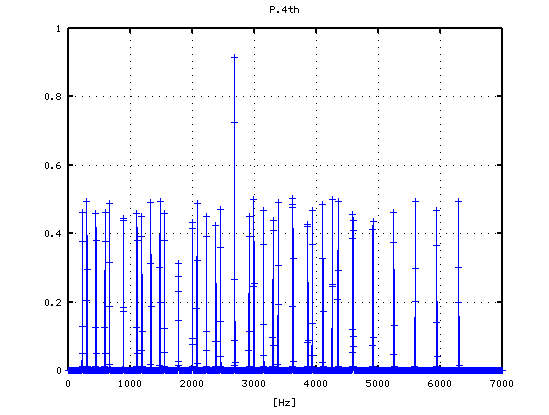 1
1
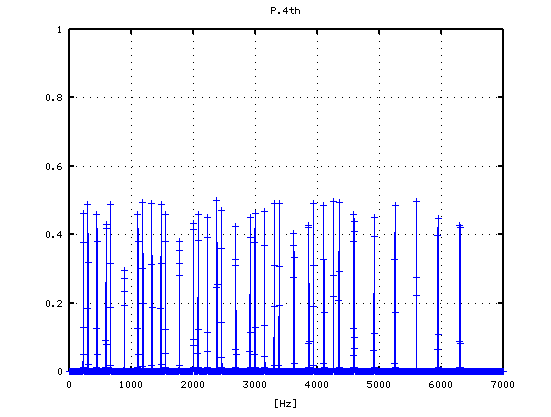 2
2
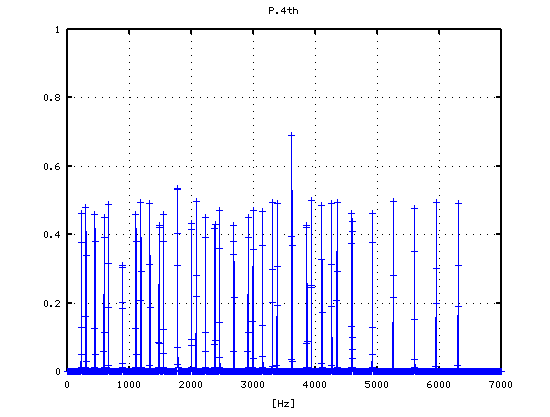 3
3
その 3Dと ピークの平均値です。
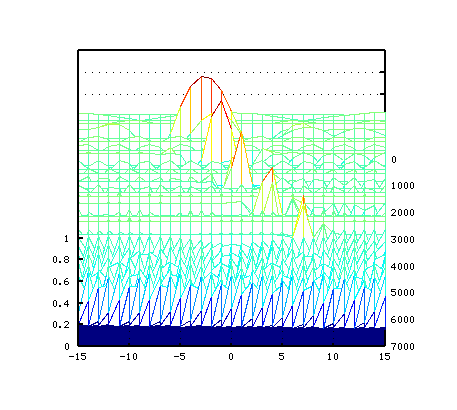
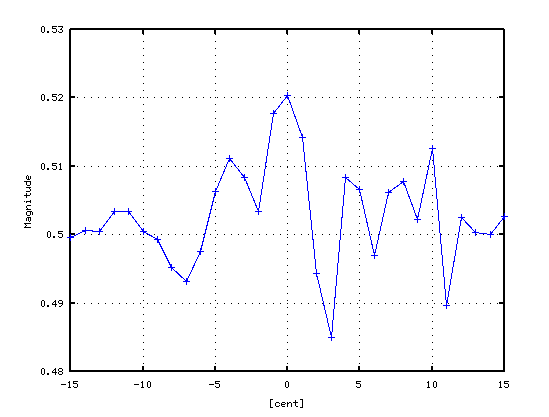
4度も -1〜-2[cent]で 4:3の倍音が合いますが D42のキーを高くして 広めにしています。
5度下(A37-D30)の場合です。
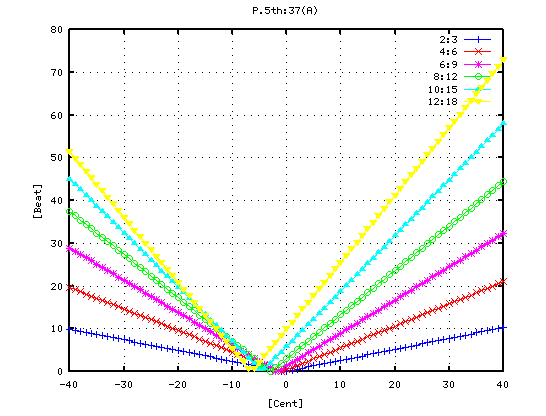
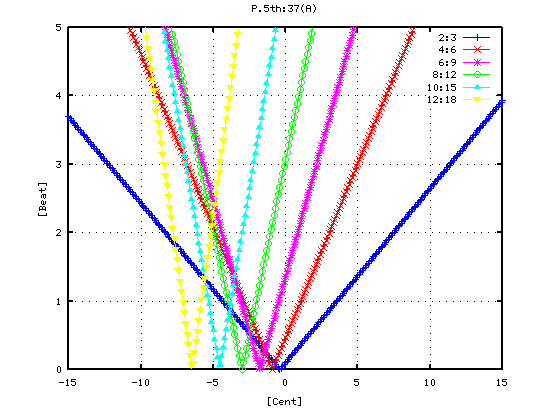
-4から +3[cent]まで 1[cent]ずつ変化させた FFTのスペクトルを見てみます。
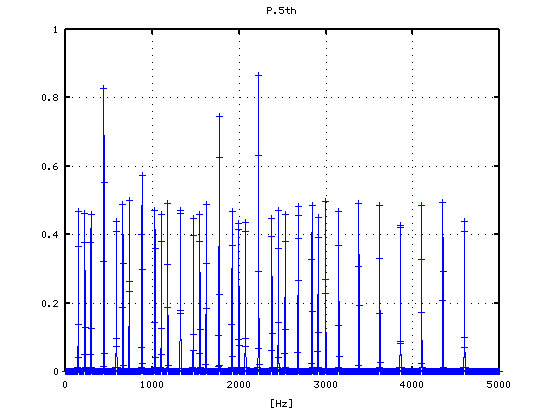 -4
-4
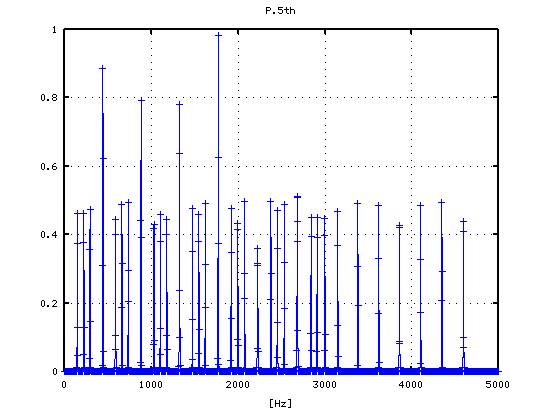 -3
-3
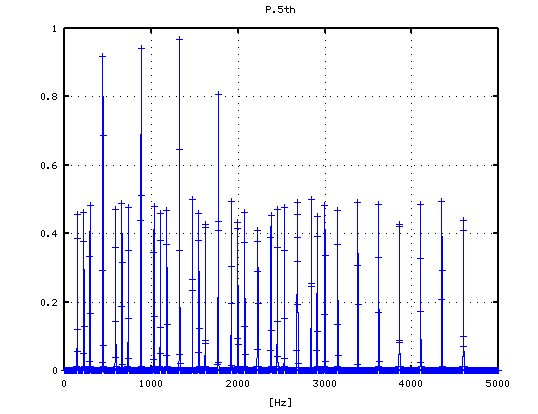 -2
-2
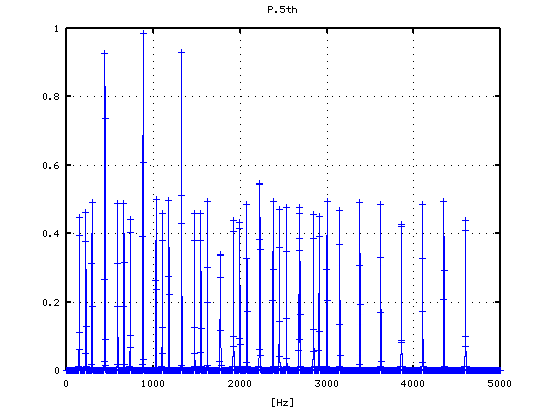 -1
-1
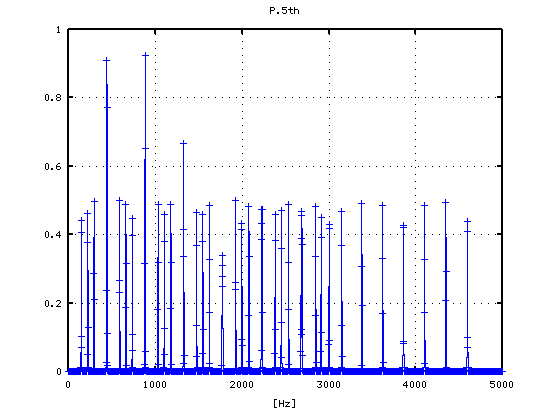 0
0
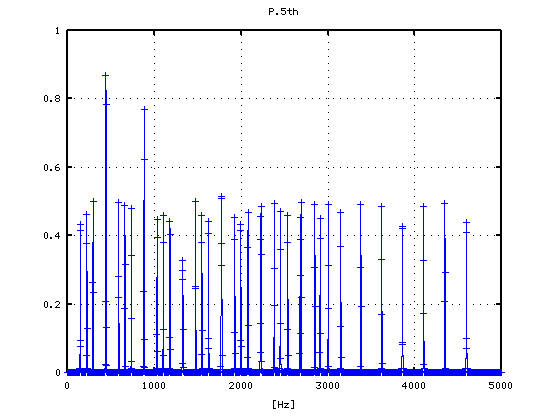 1
1
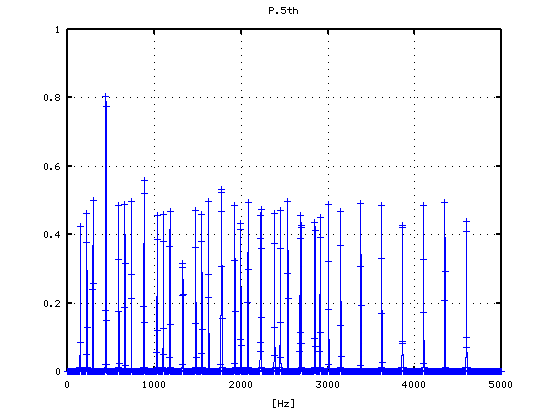 2
2
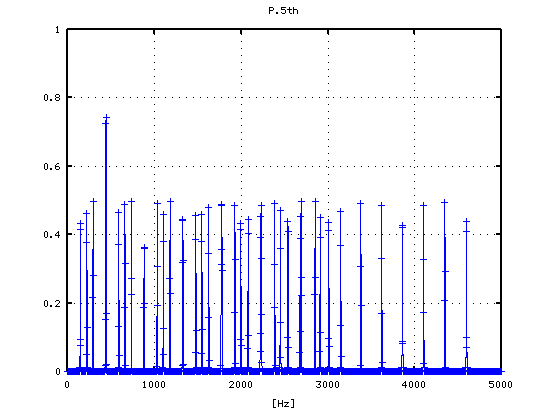 3
3
その 3Dとピークの平均値です。
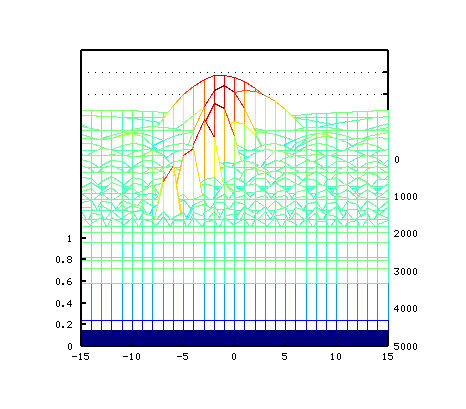
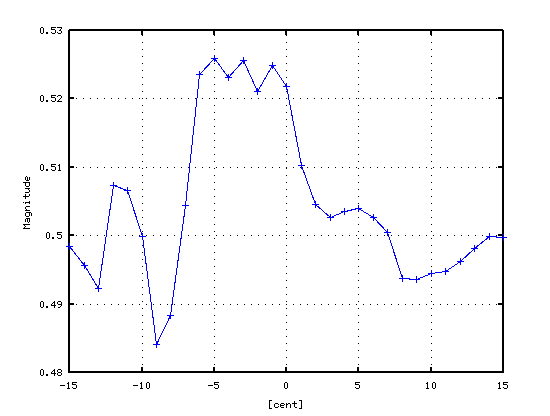
5度は -2[cent]前後で 3:2の倍音が合いますが
D30のキーを少し高くして 狭めています。
ピークの平均値では 倍音の影響が大きい事が見受けられます。
では平均律で見てみます。
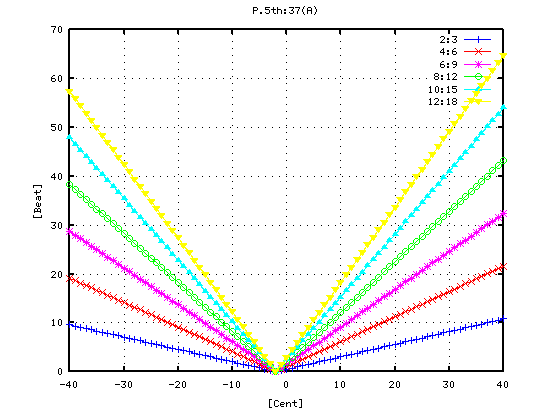
オクターブ(A37-A49)で `うなり'の数です。
それを -3から +3[cent]まで 1[cent]ずつ変化させた FFTのスペクトルで見てみます。
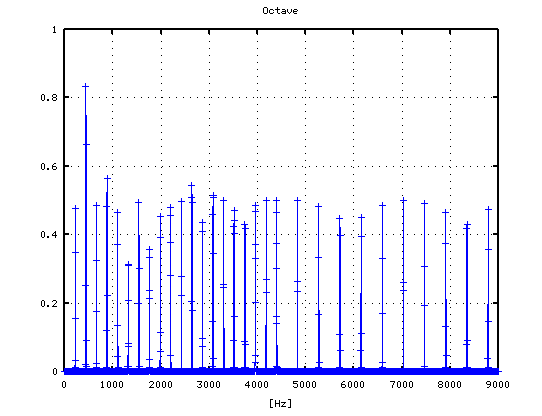 -3
-3
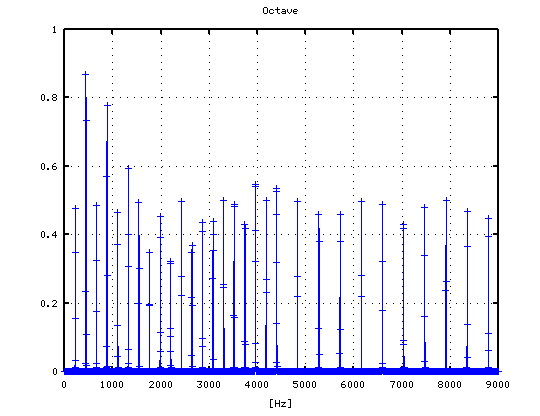 -2
-2
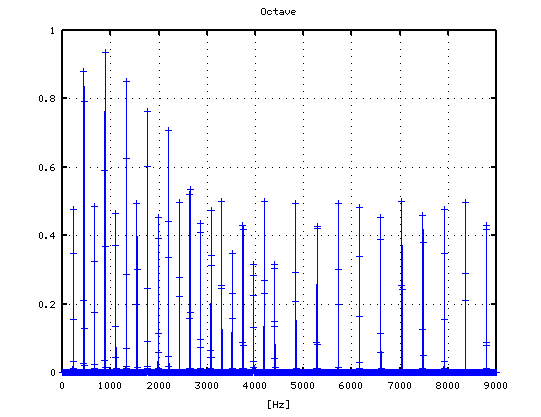 -1
-1
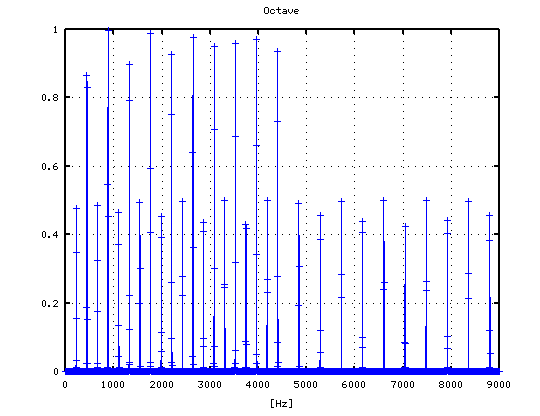 0
0
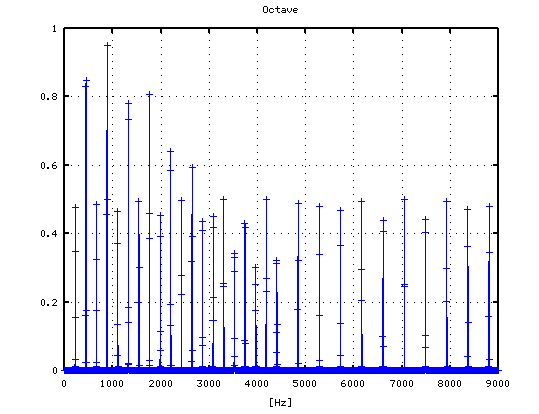 1
1
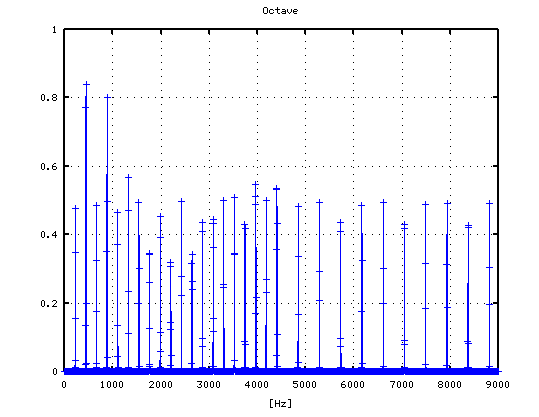 2
2
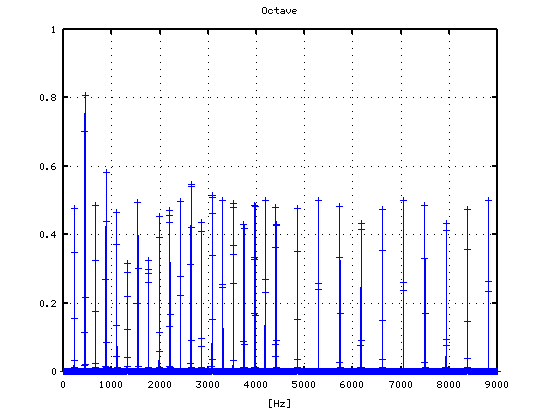 3
3
その 3Dとピークの平均値です。
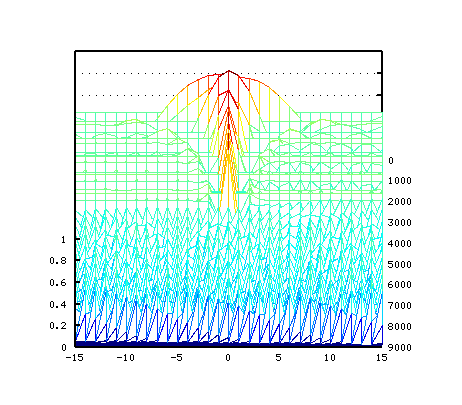
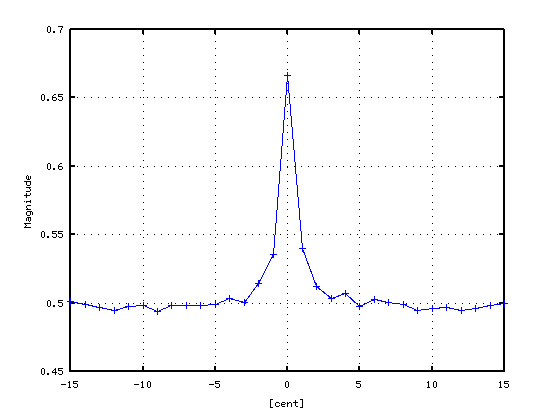
ちょうど 0[cent]で 全ての倍音が最大になるのが見えます。 つまり 全てが共鳴して`うなり'が 0となっています。
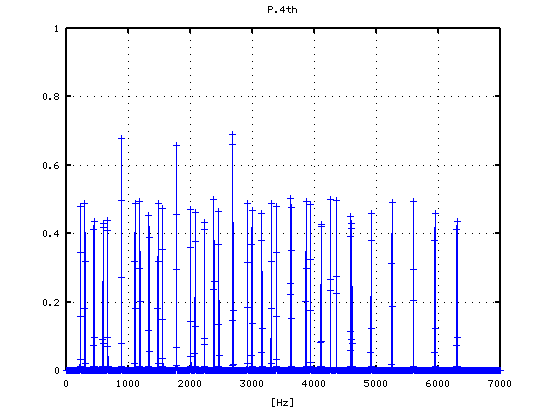
4度(A37-D42)での `うなり'の数です。
それを -3から +3[cent]まで 1[cent]ずつ変化させた FFTのスペクトルで見てみます。
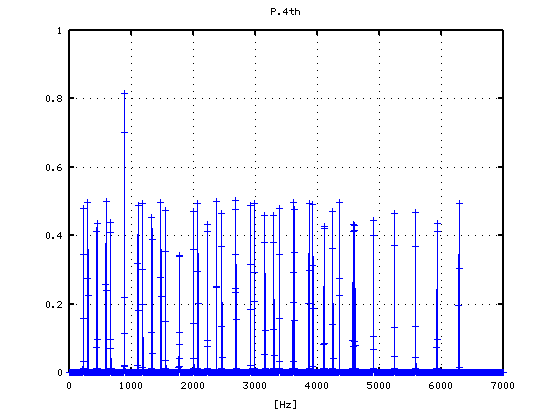 -3
-3
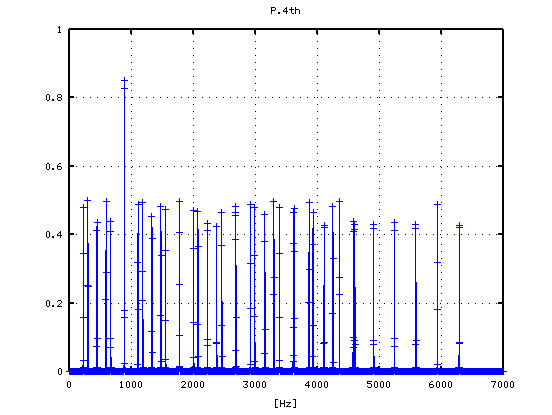 -2
-2
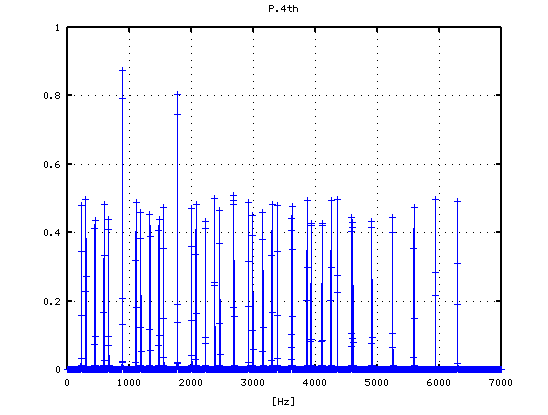 -1
-1
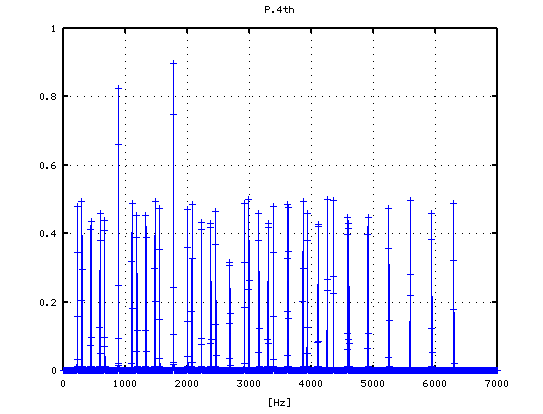 0
0
 1
1
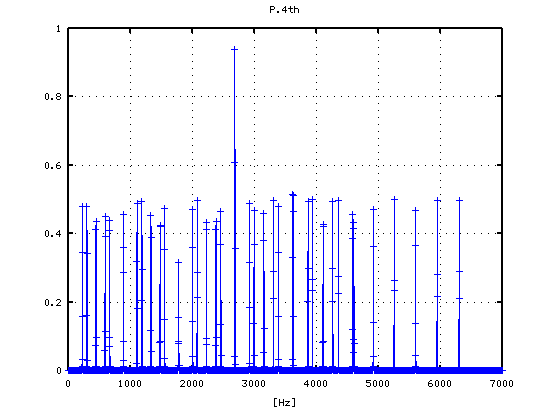 2
2
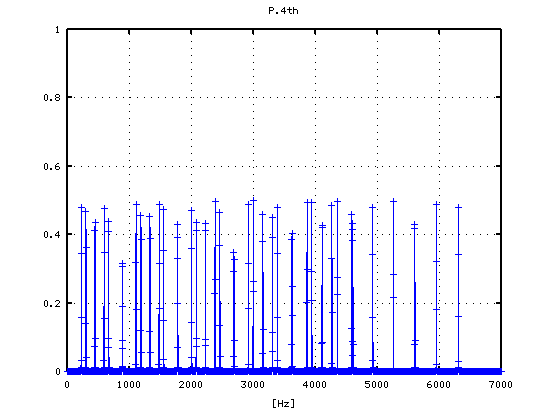 3
3
その 3Dとピークの平均値です。
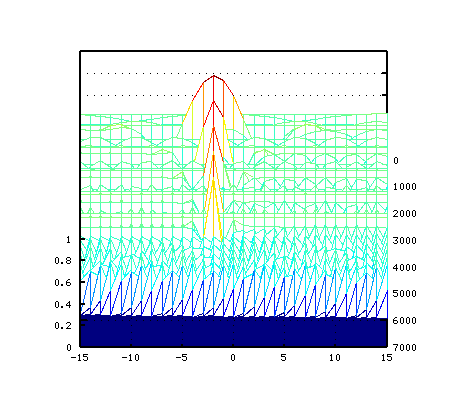
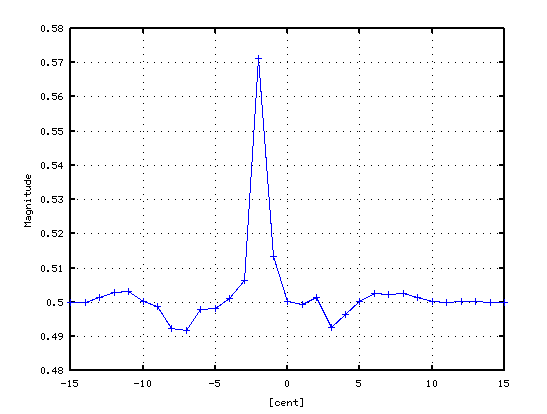
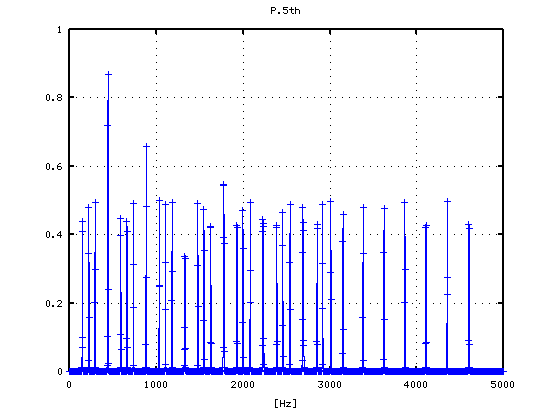
5度下(A37-D30)での `うなり'の数です。
それを -6から +1[cent]まで 1[cent]ずつ変化させた FFTのスペクトルで見てみます。
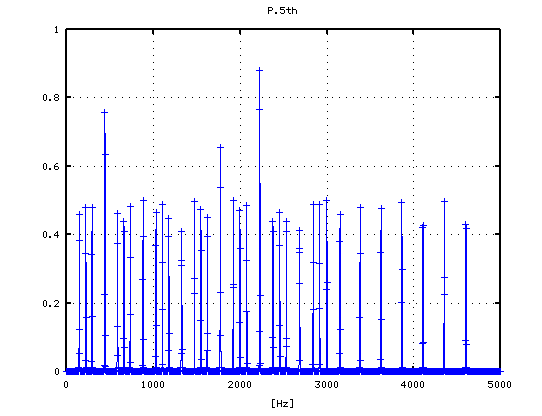 -6
-6
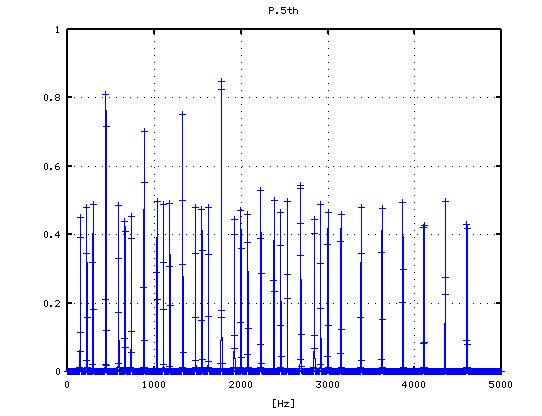 -5
-5
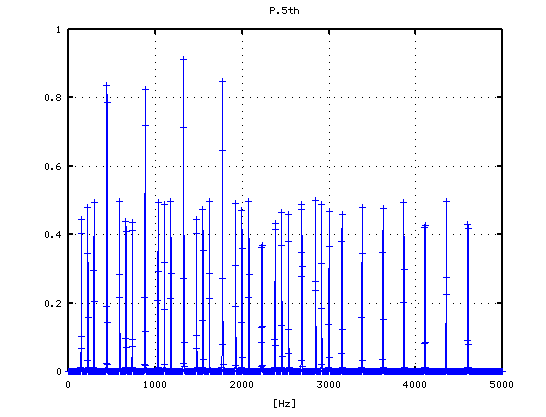 -4
-4
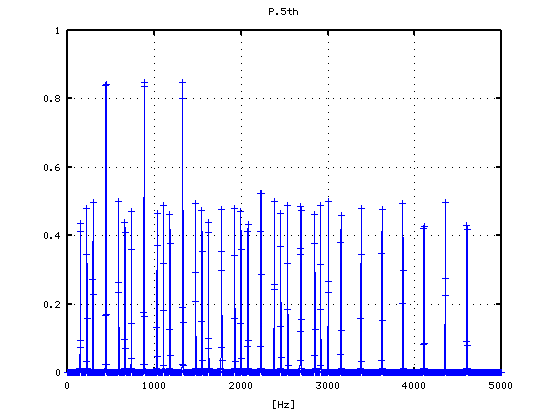 -3
-3
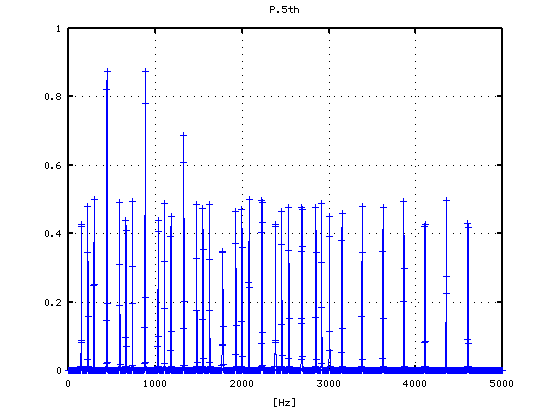 -2
-2
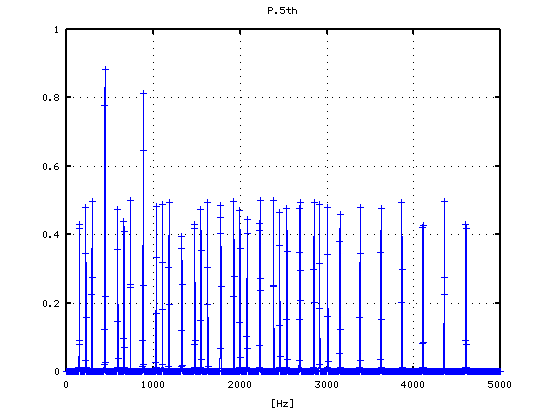 -1
-1
 0
0
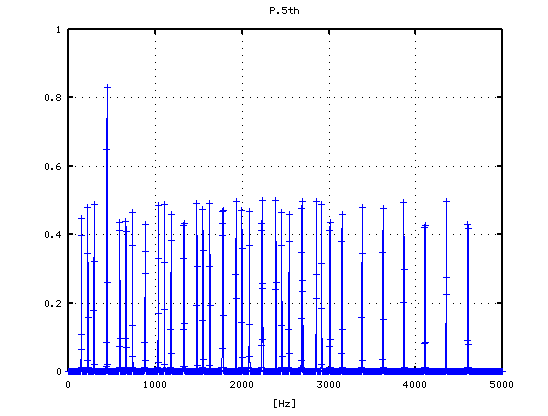 1
1
その 3Dとピークの平均値です。
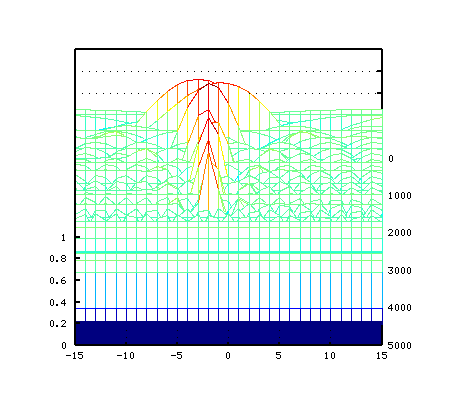
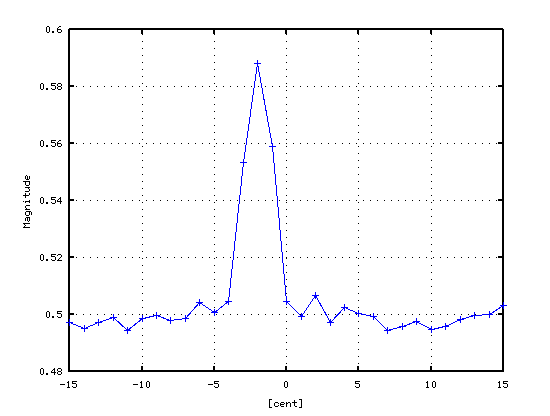
では初めの Tuningのシミュレーションに さらに弦振動のシミュレーション(打弦点と響板)を加えて見てみます。
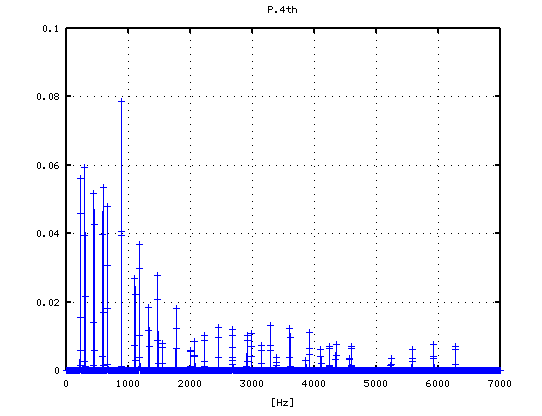
オクターブ(A37-A49)で -4から+3[cent]です。
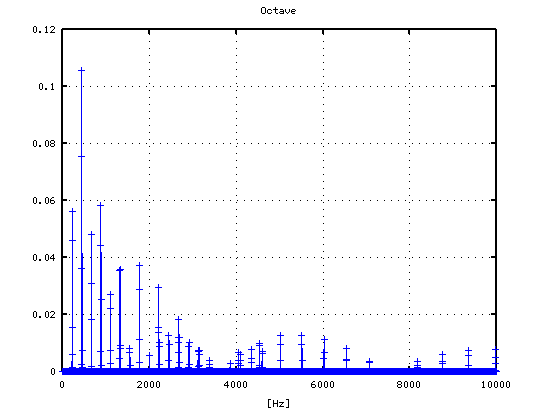 -4
-4
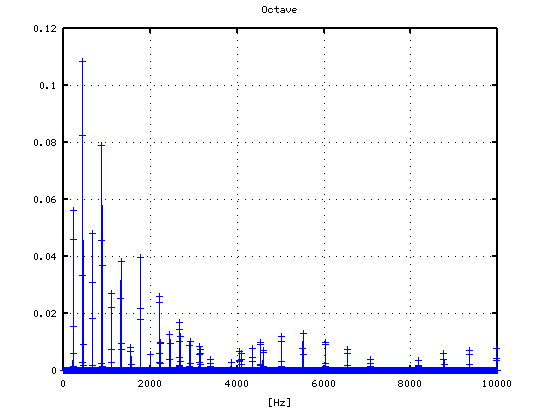 -3
-3
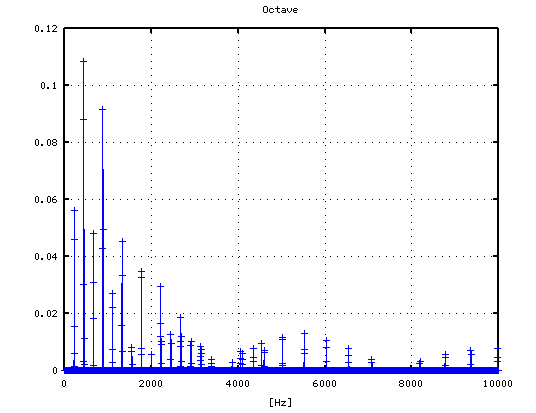 -2
-2
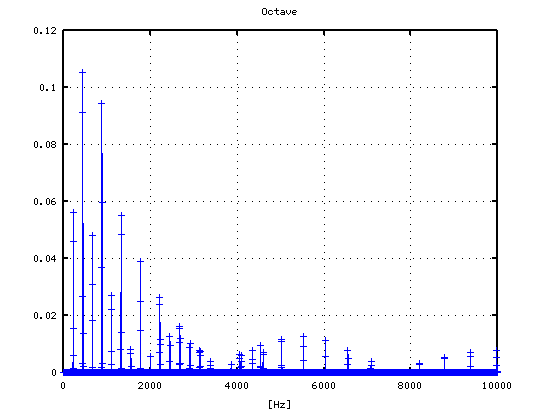 -1
-1
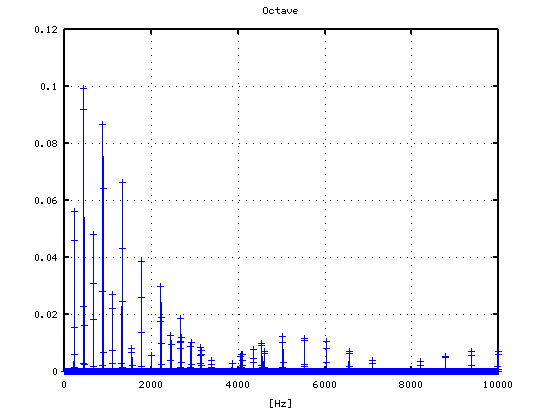 0
0
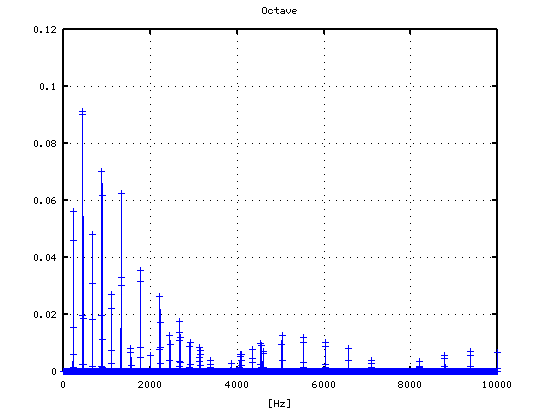 1
1
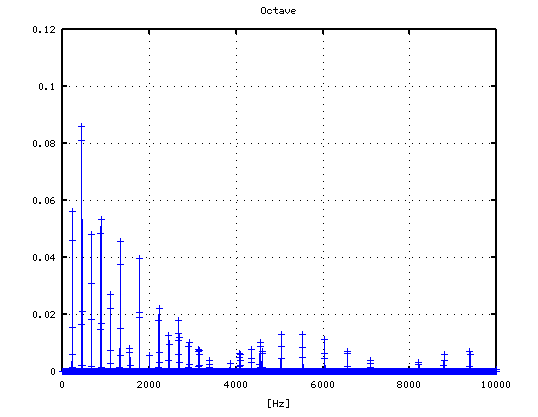 2
2
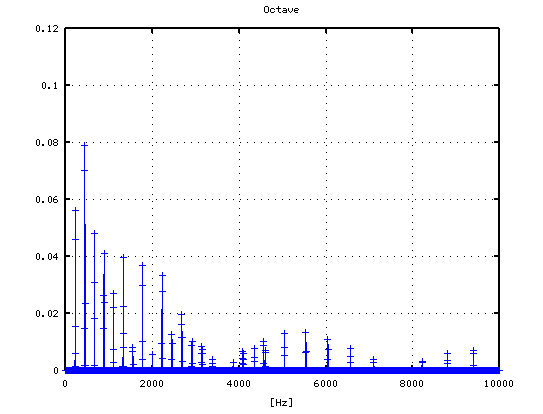 3
3
その 3Dとピークの平均値です。
弦振動が加わる事で 倍音の音量は下がります。
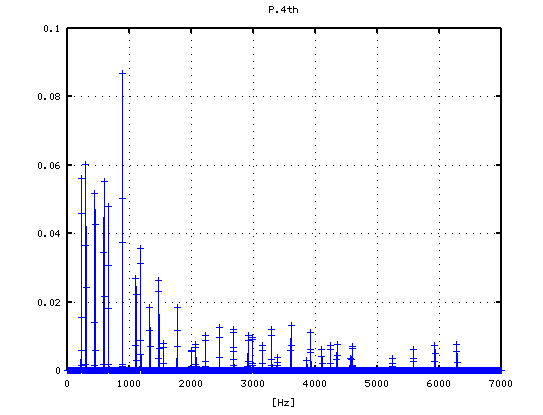
4度(A37-D42)で -4から+2[cent]です。
 -4
-4
 -3
-3
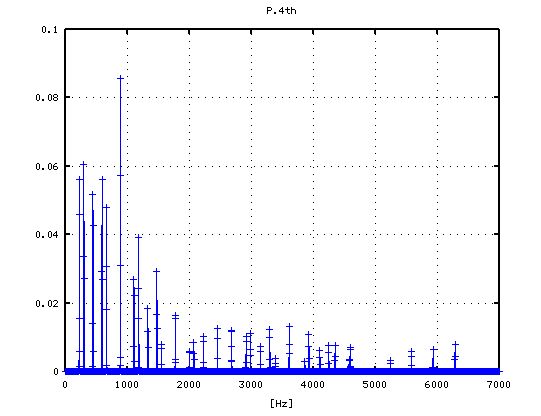 -2
-2
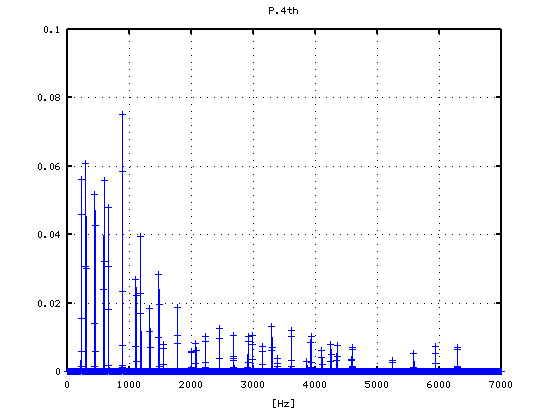 -1
-1
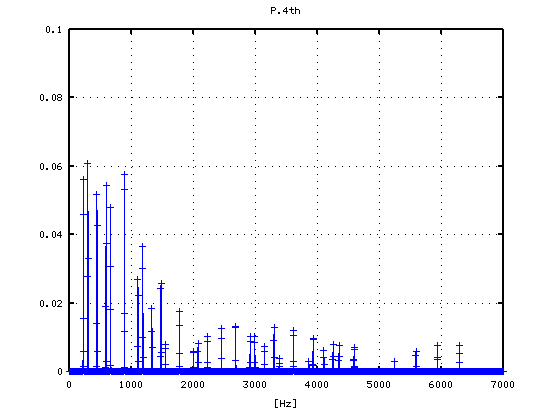 0
0
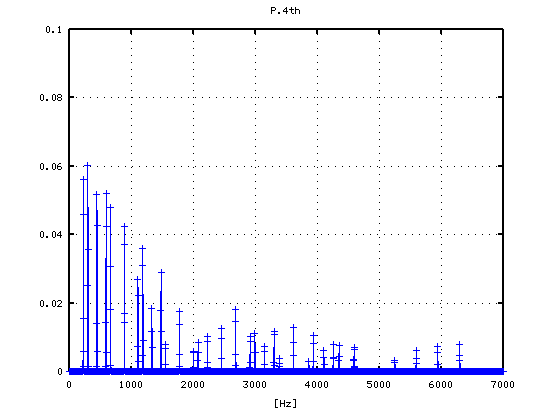 1
1
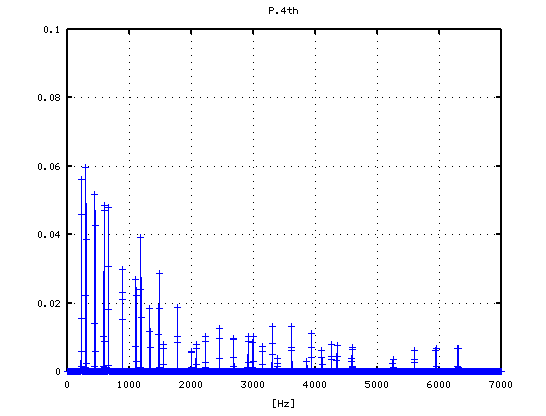 2
2
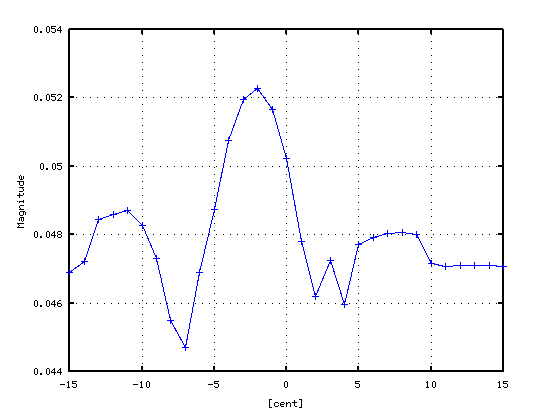
その 3Dとピークの平均値です。
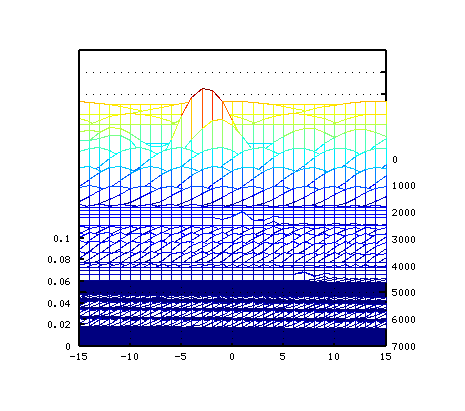
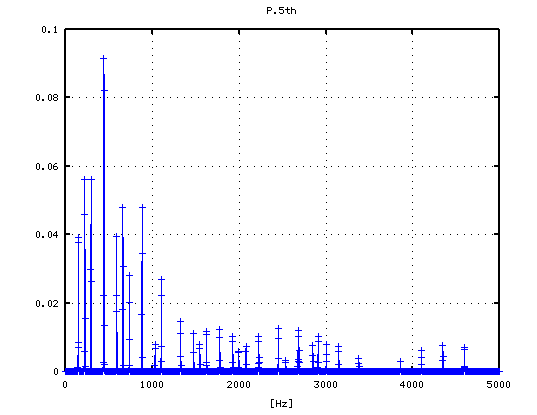
5度下(A37-D30)で -4から+3[cent]です。
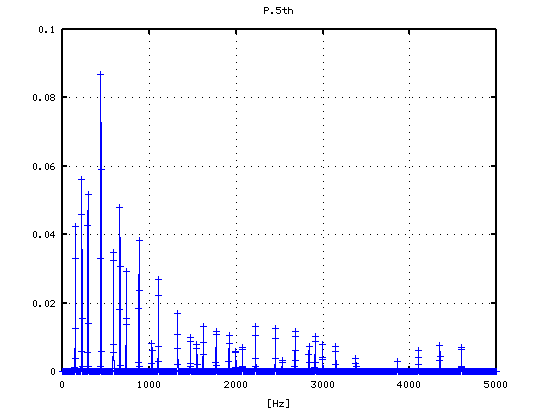 -4
-4
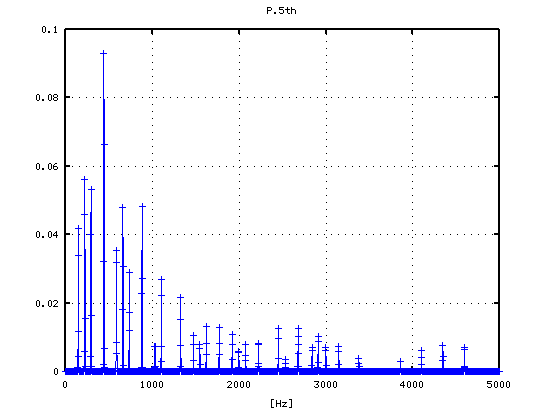 -3
-3
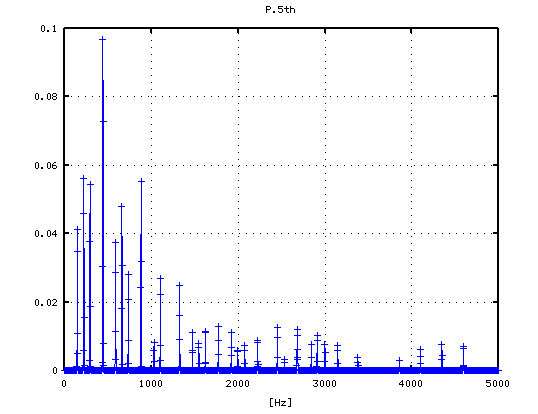 -2
-2
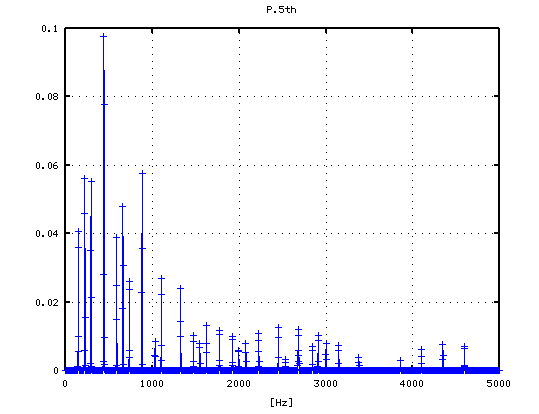 -1
-1
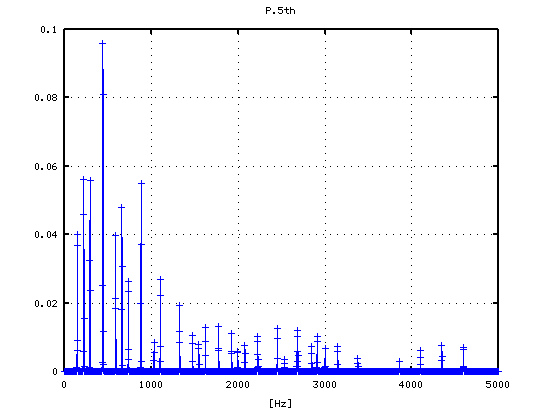 0
0
 1
1
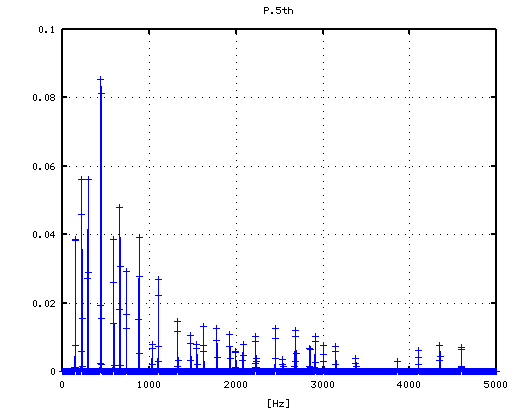 2
2
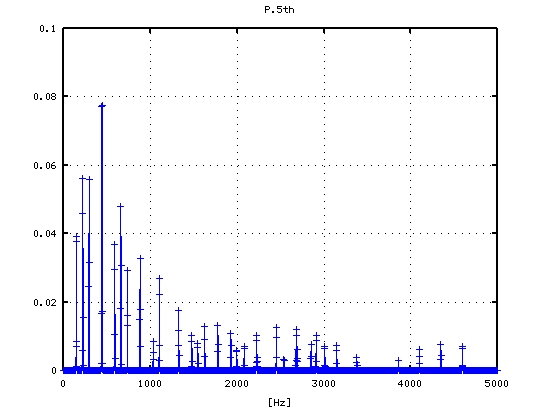 3
3
3Dとピークの平均値です。
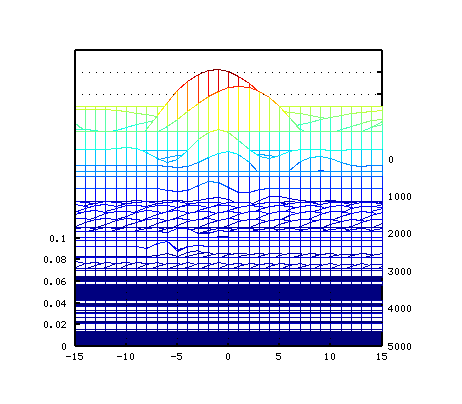
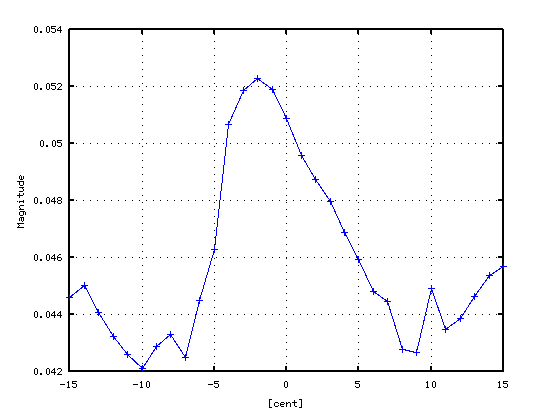
ピークの平均値では 倍音の減少によって 変化は滑らかで明瞭になっています。
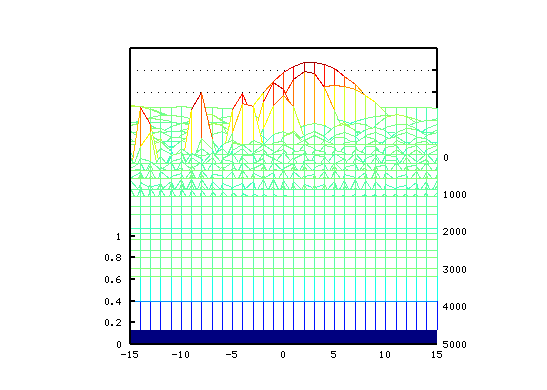
A37キーから下へオクターブを作る場合です。
(低い周波数に対して より分解能がよくなるように変えています。
-15[cent]から+15[cent]です。)
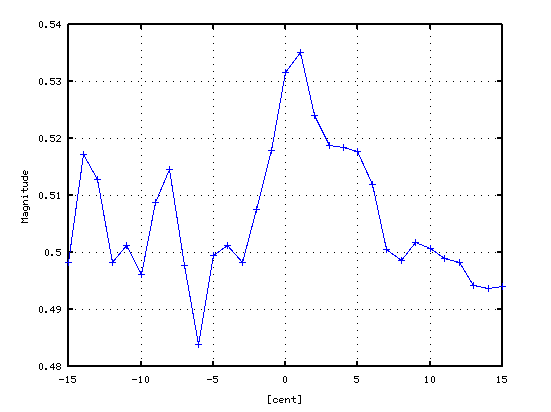
A25キーから下へのオクターブです。