音声の周波数成分を調べる方法に「フーリエ変換」と言うものがあります。
(難しい数式は省略;)
光のように 音をその周波数成分のスペクトルとして分解するもの
とでも言えるでしょうか。
その処理方法に「高速フーリエ変換」(Fast Fourier Transform : FFT)
があります。
(以下では 波形作成プログラムで数値データを作り それをFFTプログラム(C言語)で処理したデータを グラフ再生ツール (GNUPLOT)で画像を作っています)
初めに代表的な波形を見て見ましょう。
(図をクリックして下さい。拡大されます)
先ず矩形波です。
(左が信号波形のグラフ・右がそのFFT処理のグラフです)
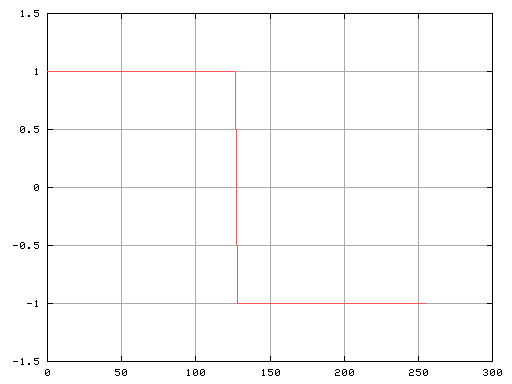 Fig-a
Fig-a
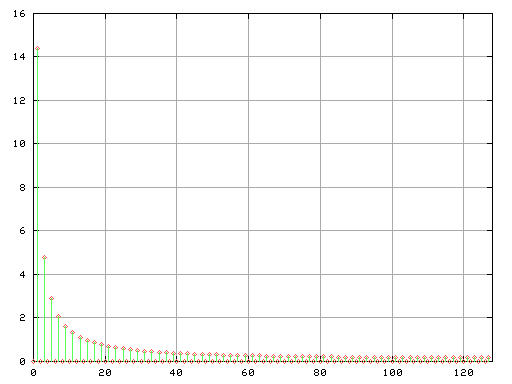 Fig-b
Fig-b
(この例では周波数は分かりやすく 1[Hz]で行っていますので
FFT画像は横軸に 0〜128倍の高調波成分の表示となります)
矩形波は1,3,5...と奇数倍の高調波で作られています。
次は三角波です。
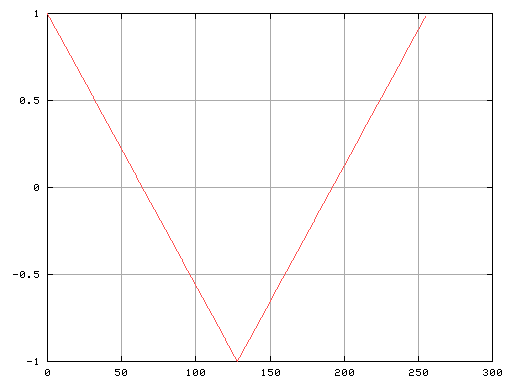 Fig-d
Fig-d
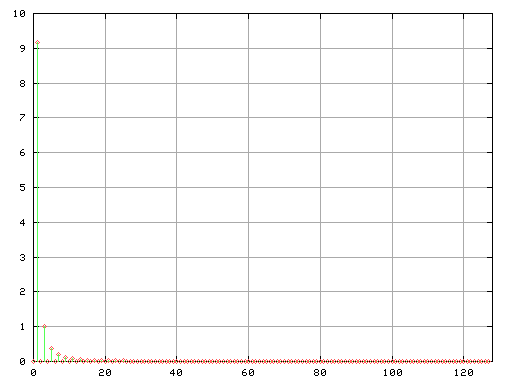 Fig-e
Fig-e
矩形波と同じく奇数倍ですが 高調波になるほど少なくなっています。
次はノコギリ波です。
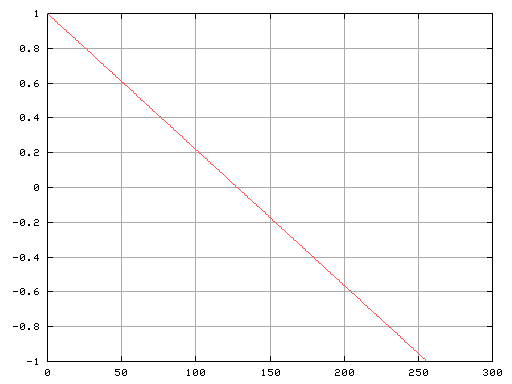 Fig-f
Fig-f
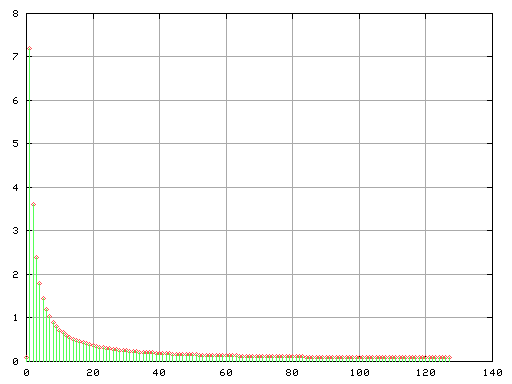 Fig-g
Fig-g
矩形波・三角波と違い倍音は順にあります。
(0次の音?と思うかも知れませんが直流成分(波形の平均値)です.)
最後にインパルス波です。
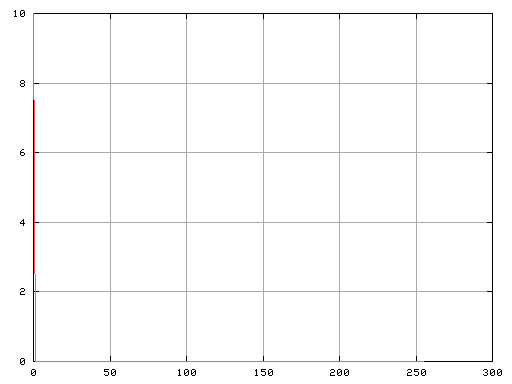 Fig-h
Fig-h
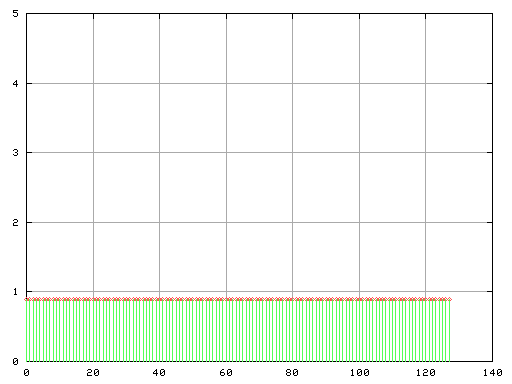 Fig-i
Fig-i
インパルス波はすべての倍音成分を含みしかも全て同じ大きさです。
例えばあるサイン波(Fig-1)をフーリエ変換すると Fig-2 の様になります。
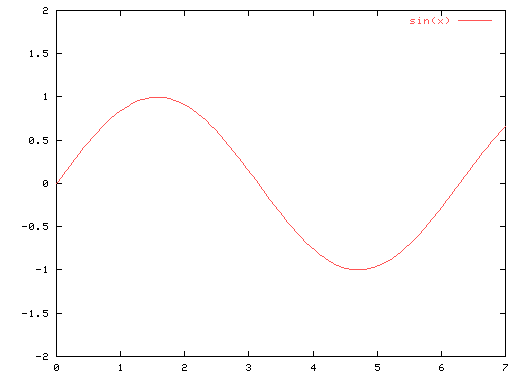 Fig-1
Fig-1
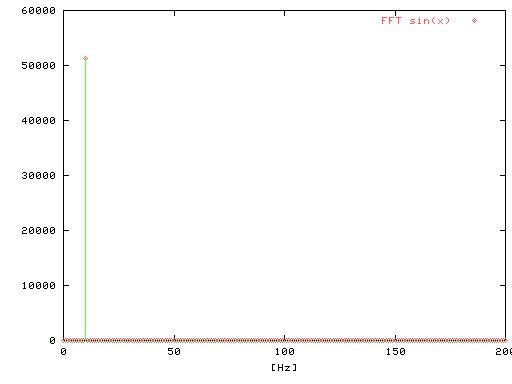 Fig-2
Fig-2
これは単純な10[Hz]のサイン波なので
10[Hz]の成分のみがあることを示しています。
では 20[Hz]のサイン波はどうなるでしょう?
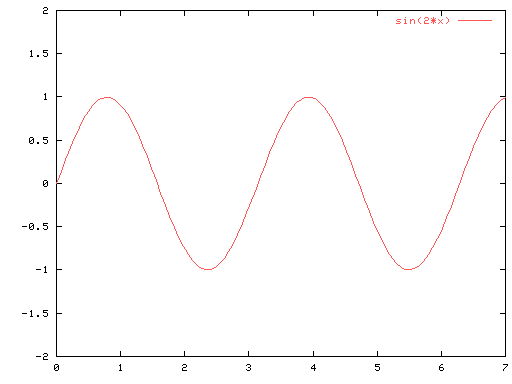 Fig-3
Fig-3
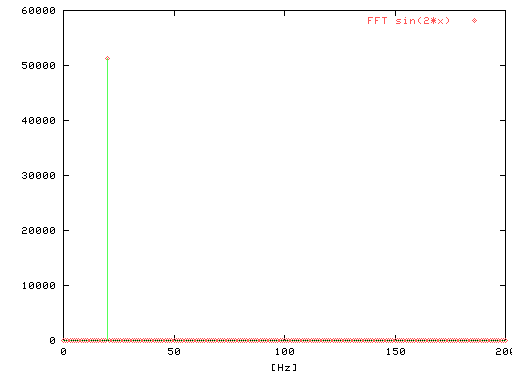 Fig-4
Fig-4
サインカーブは2倍になりましたが
スペクトル成分は 20[Hz]に移るだけです。
今度は二つの波 10[Hz]と 20[Hz]を合成して見ましょう。
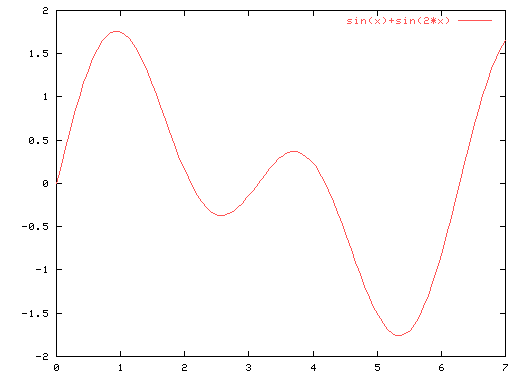 Fig-5
Fig-5
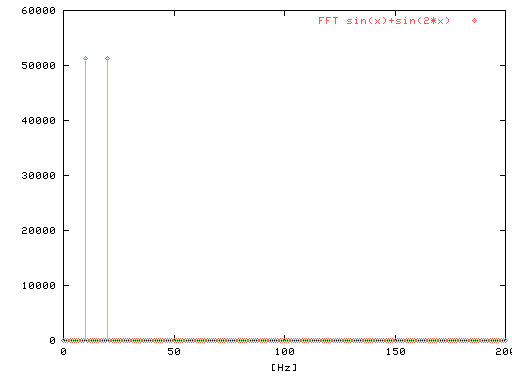 Fig-6
Fig-6
二つの波は合成されましたが そのスペクトルは 10[Hz]と
20[Hz]に分析されています。
では 16倍音まであるサイン波形はどうなるでしょう?
1から16倍までの波形を Fig-7 に(振幅は少しずつ減少させてあります)
その合成波を Fig-8・そのフーリエ変換は Fig-9 です。
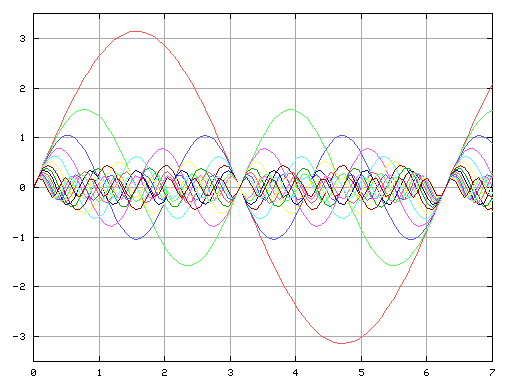 Fig-7
Fig-7
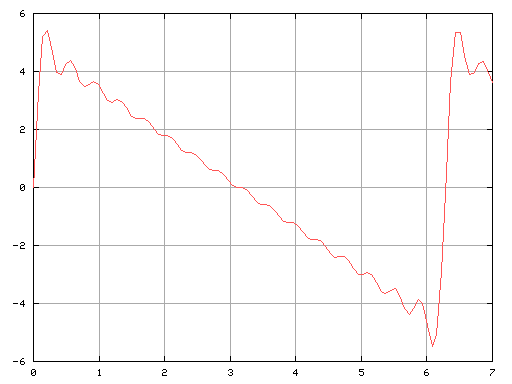 Fig-8
Fig-8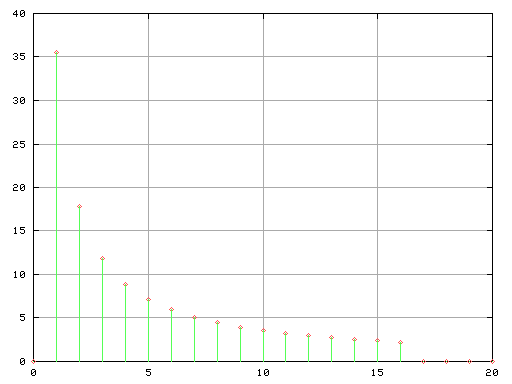 Fig-9
Fig-9
倍音成分のスペクトルが振幅の量に比例して表されます。
倍音を持たない二つの波形の合成はどうなるでしょう?
20[Hz]と 30[Hz](五度音程 2:3)での合成波とそのスペクトルです。
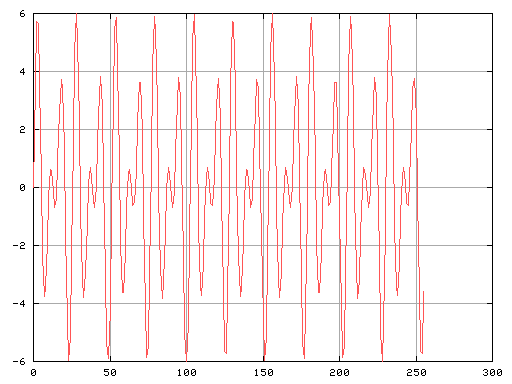 Fig-10
Fig-10
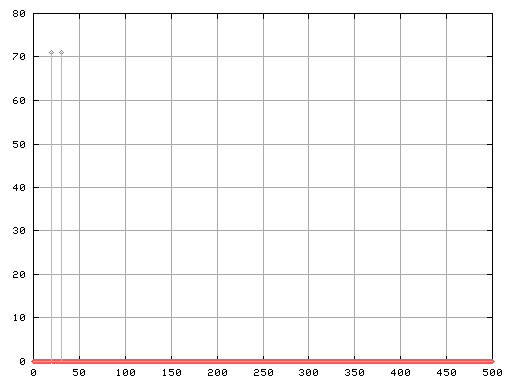 Fig-11
Fig-11
では次に 16倍音を持つ 20[Hz]と 30[Hz]の合成です。
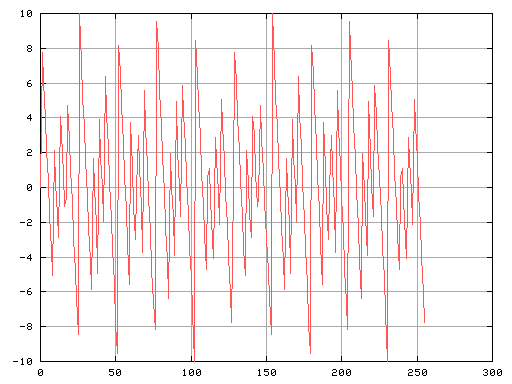 Fig-12
Fig-12
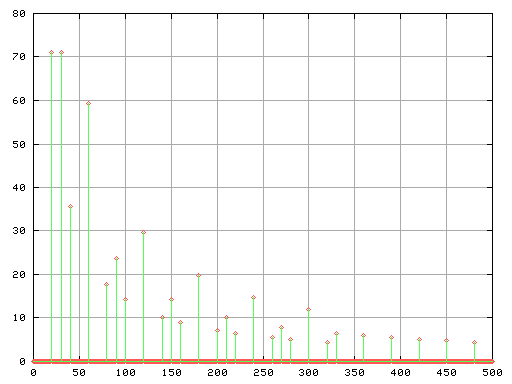 Fig-13
Fig-13
共鳴している60[Hz]・120[Hz]・180[Hz]・240[Hz]・300[Hz]で
振幅が増えているのが分かります。
20[Hz]と21[Hz]ではどうでしょう?
 Fig-14
Fig-14
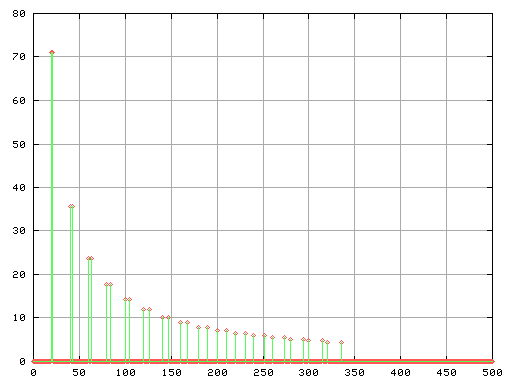 Fig-15
Fig-15
波形の Fig-14では周期 1の'うなり'が見えますが
FFTの Fig-15に 1[Hz]は現れてはいません。
'うなり'は二つの音の差から生じる音量の'うねり'の様に言われていますが
「倍音成分を含む音では'うなり'はその共鳴する倍音成分の音量の増加」
もあるのではないでしょうか?
(※v0.3)これまでの波形に幾つかプラスしました。
「Chirp」(チャープ)は幅広い周波数を含んでいます。
[Filter]でその制限を見てみて下さい。
「7.0Sine」は丁度の振幅の信号で「6.7Sine」は少しずれた信号です。
[Window]でそのずれをカバーしようとする所を見てみて下さい。
参照 >高速フーリエ変換シミュレーター (FFT Simulator)
インハーモニシティ(サンダーソン氏の式) で FFTのシミュレーションを行います。
参照>インハーモニシティについて (Inharmonicity)
参照>インハーモニシティ・FFT2 (Inharmonicity FFT2)
【インハーモニシティ無し】の場合です。 (大きさの変化を見る為 倍音は等量にしてあります)
オクターブ(25<A> 109.513[Hz] -> 37<A> 219.516[Hz] 20倍音まで)で見てみます。
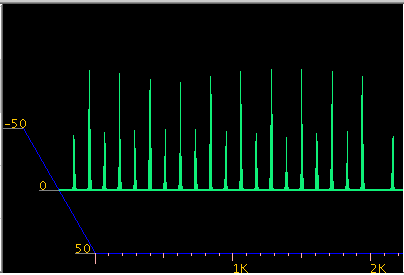 Fig-16
Fig-16
2・4・6...と奇数倍でスペクトルの増加があります。
上側のキーを1セントづつ ±50セントまで変化させて
前後に重ねて見ます。
参照>FFTによる`うなり'
(BFFT3)
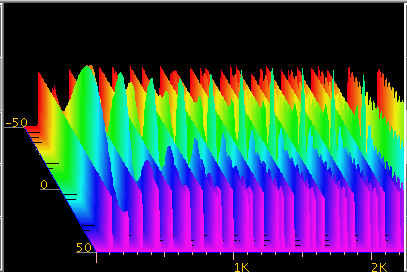 Fig-17
Fig-17
中央の 0セントで全ての倍音が最大になります。
純正5度(25<A> 109.513[Hz] -> 32<E> 164.308[Hz])です。
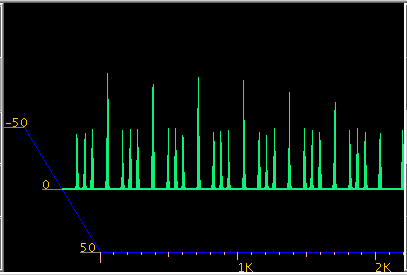 Fig-18
Fig-18
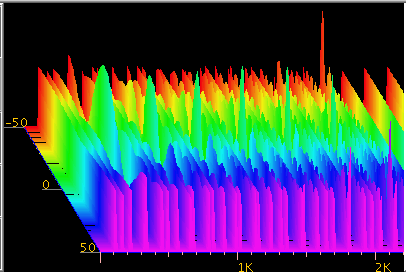 Fig-19
Fig-19
【インハーモニシティあり】の場合です。
オクターブです。
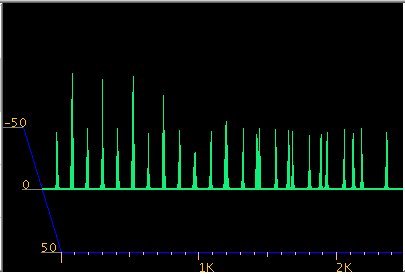 Fig-20
Fig-20
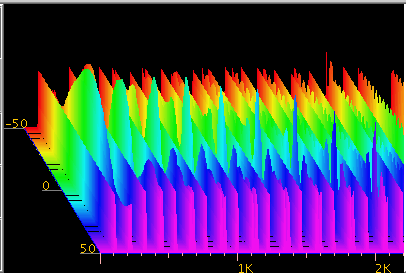 Fig-21
Fig-21
高い倍音がプラス側(青色)にずれて 最大になるのが見えます。
下側のキーを変化させると マイナス側(赤色)にずれて 最大になります。
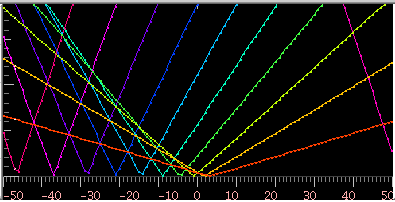 Fig-22
Fig-22
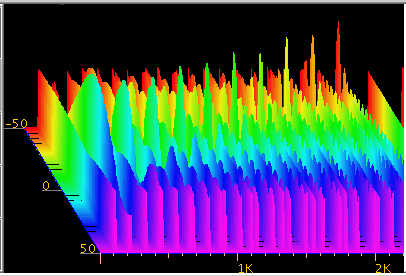 Fig-23
Fig-23
5度です。
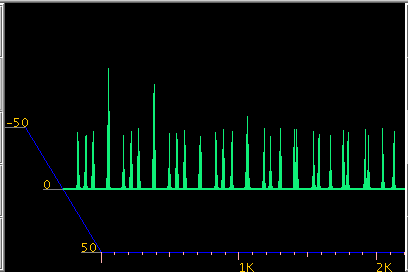 Fig-24
Fig-24
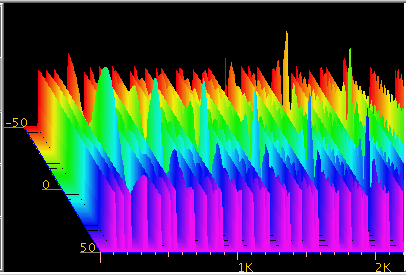 Fig-25
Fig-25
インハーモニシティがある場合では倍音の取り方 (聞き方)によって共鳴点が異なって来ます。
(変更履歴:
v0.3['20/07/19] HTML5に変更しました。
Wave信号を見る Beat.jsを追加しました。
v0.2.2 ['15/07/18] テキストの表示を少し変更しました。
v0.2.1 ['13/06/08] cssファイルを別にしました。)