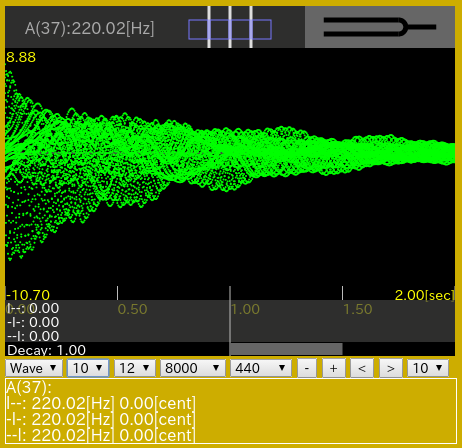
ピアノ弦のインハーモニシティありの場合を Inharmonicity FFT(IFFT) を使って見てみます。
例えば A(25) 110[Hz]で インハーモニシティ値の異なる
2本の弦を合わせるとします。
Ch.1は(0.993)に固定し Ch.2は半音下から100[cent]上げて(0.099)・(0.09)・
(0.08)と変えた場合の`うなり'です。
基音で`うなり'を 0にするため Ch.2は数セントずれます。 (0.099)の目盛は最大にしてあります。(0.0993)の時のうなりは全て 0ですから 省略しました。
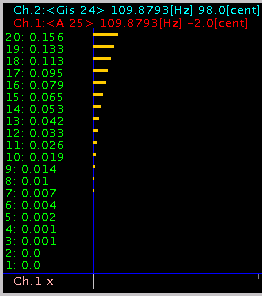 0.099
0.099
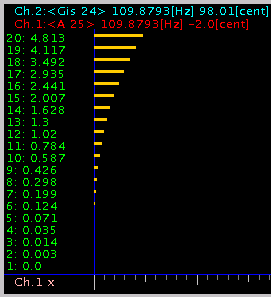 0.09
0.09
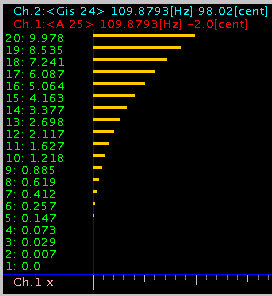 0.08
0.08
その時の FFTでのグラフです。
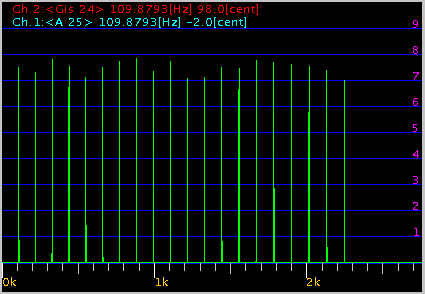 0.099
0.099
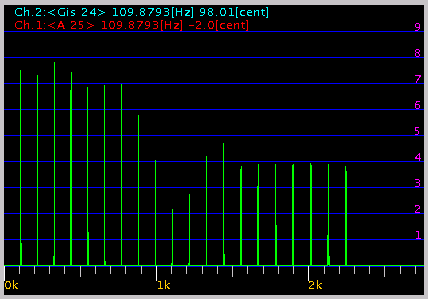 0.09
0.09
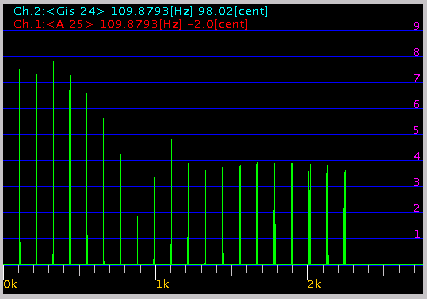 0.08
0.08
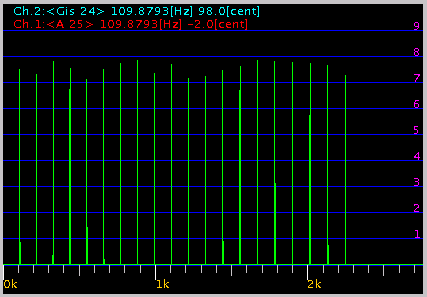 0.0993
0.0993
実際のピアノでは どうでしょう?
| # | Left | Right | Balance |
|---|---|---|---|
| 1 | 0.1767 | 0.1812 | 0.0045 |
| 2 | 0.1718 | 0.1763 | 0.0045 |
| 3 | 0.1378 | 0.1393 | 0.0015 |
| 4 | 0.1408 | 0.1445 | 0.0037 |
| 5 | 0.1185 | 0.1212 | 0.0027 |
| 6 | 0.1158 | 0.1185 | 0.0027 |
| 7 | 0.1036 | 0.1060 | 0.0024 |
| 8 | 0.1024 | 0.1052 | 0.0028 |
| 9 | 0.1012 | 0.1041 | 0.0029 |
| 10 | 0.1078 | 0.1108 | 0.003 |
| 11 | 0.1075 | 0.1105 | 0.003 |
| 12 | 0.1081 | 0.1112 | 0.0031 |
| 13 | 0.1092 | 0.1119 | 0.0027 |
| 14 | 0.1102 | 0.1135 | 0.0033 |
| 15 | 0.0968 | 0.0993 | 0.0025 |
| 16 | 0.0970 | 0.1020 | 0.005 |
| 17 | 0.0643 | 0.0643 | 0 |
| 18 | 0.0667 | 0.0667 | 0 |
| 19 | 0.0697 | 0.0697 | 0 |
差を(0.0033)として A(13) 55[Hz] Ch.1 (0.1393)・Ch.2 (0.136)の場合のユニゾンの`うなり'を -1〜+3[cent]に変化させて見ます。
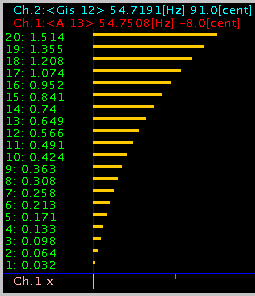 -1
-1
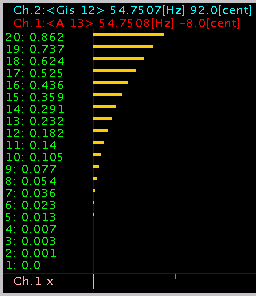 0
0
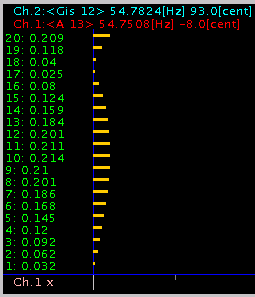 1
1
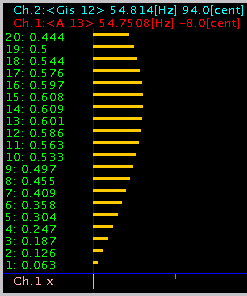 2
2
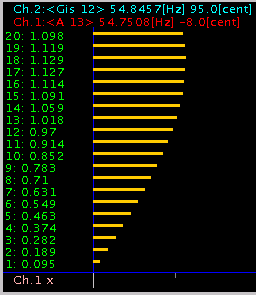 3
3
その時の FFTでのグラフです。
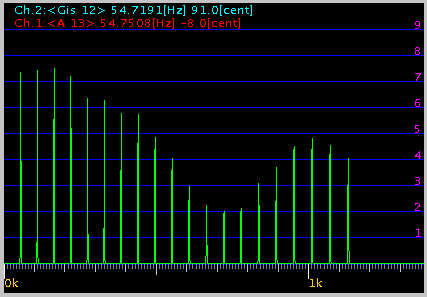 -1
-1
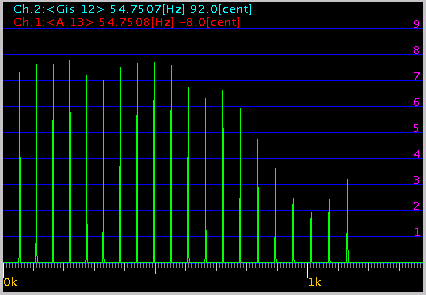 0
0
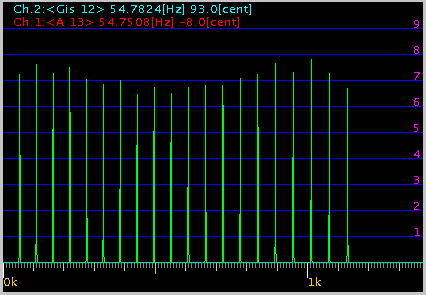 1
1
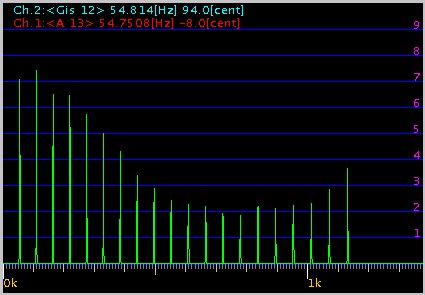 2
2
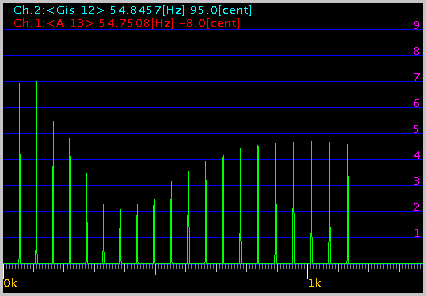 3
3
もう少しインハーモニシティ値が異なる(0.0093)とどうなるでしょう?
Ch.2を (0.13)にした場合 -1〜+4[cent]まで変化させて見ます。
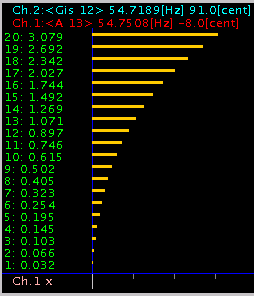 -1
-1
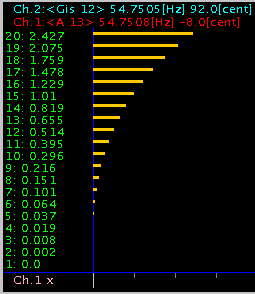 0
0
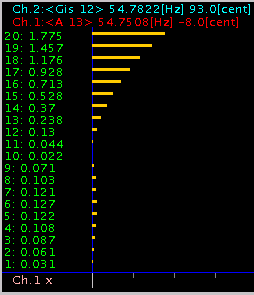 1
1
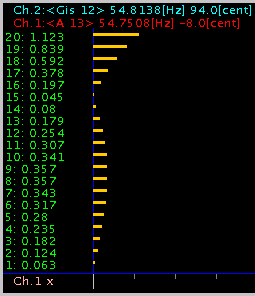 2
2
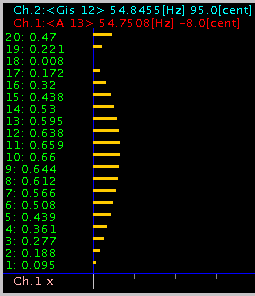 3
3
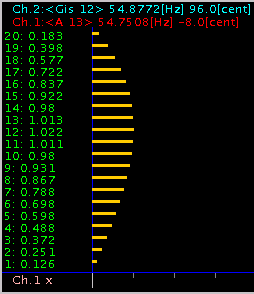 4
4
その時の FFTでのグラフです。
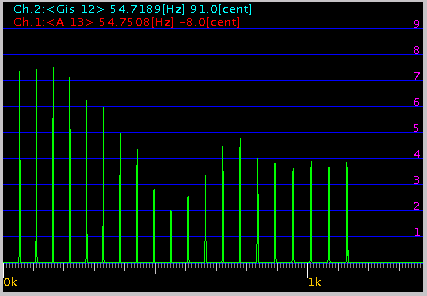 -1
-1
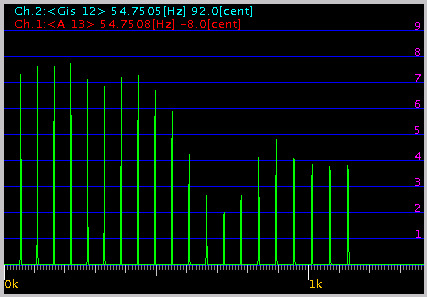 0
0
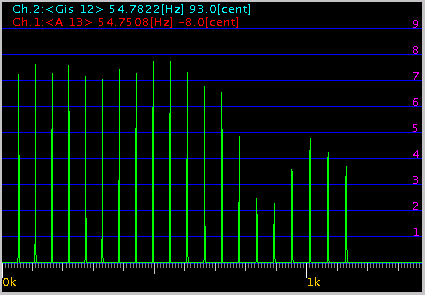 1
1
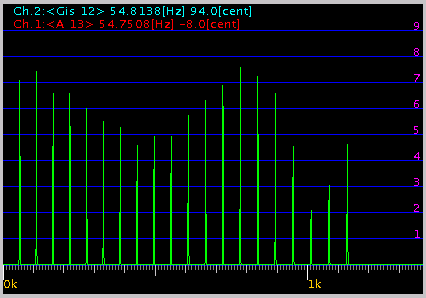 2
2
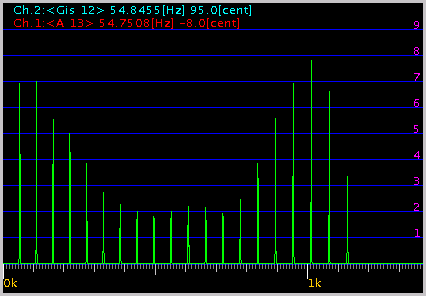 3
3
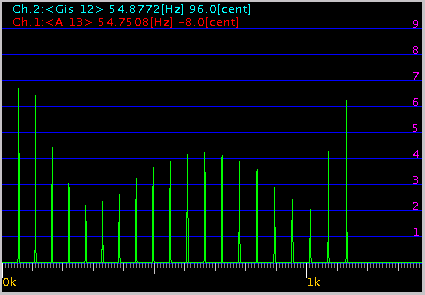 4
4
インハーモニシティ差のある場合は
ユニゾンでもオクターブ・5度・3度でも
和音はこのような倍音の`うなり'の変化の仕方をします。
例えば 5度(3:2) A(25):E(32)の場合。
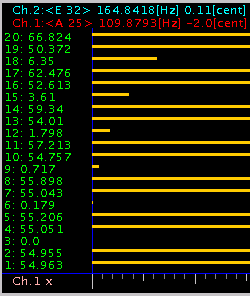
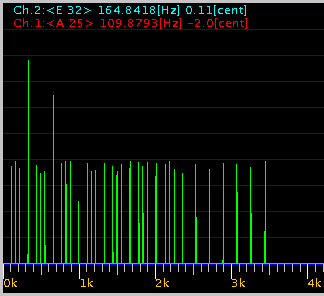
共鳴する A(25)の 3の倍数の倍音に これまでに見られたような`うなり'の変化が見られます。
共鳴はインハーモニシティ差が大きい程 同調する倍音の幅 (数 or 高さ)が狭くなります。
またインハーモニシティ差のある場合の共鳴点は 基音でピタリと合わせるよりやや高めの方がスペクトル的(?)には 音量が豊かになるように見受けられます。
(変更履歴:
v0.1.2 ['14/11/23] HTML5版を追加しました。
「エンベロープで見るユニゾンのシミュレーション
(Unison Simulation of Envelope)」

HTML5版です。
v0.1.1 ['13/06/01] cssとJavaScriptファイルを別にしました。)