それに当てはまる式を求める為に,統計解析や回帰分析で使われている
最小2乗法(の指数関数 - 計算方法の説明は省略;)を使って
y = a exp(b x)と言う式の値 a = 1.05409, b = 0.95361を得ます。
その式をデータと重ねて表示して見ます。
(y軸(上下方向)は対数目盛になっています)
- イマジナリー・ピアノ
それを
Designで作成したイマジナリー・ピアノ
(インハーモニシティ値が対数グラフで直線的に変化しているもの)
で試して見ます。
初めに「Java Tuner(JT)」
で見た [Design]のインハーモニシティ値です。
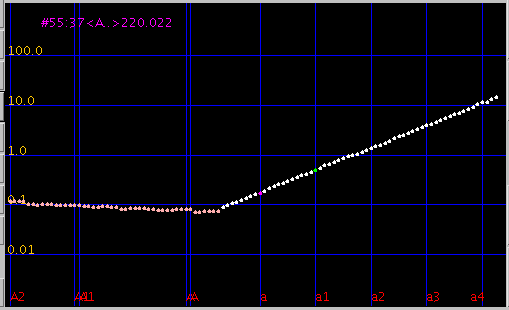 Fig.2
Fig.2
そこから4つのデータを取り出します。
| Key# | Inha. |
|---|
| 13 | 0.098 |
| 25 | 0.083 |
| 37 | 0.173 |
| 49 | 0.499 |
それから芯線の部分と巻き線の部分を別々に最小2乗法[I2TC]で計算して
データを選択して2つの直線にします。
比較の為[JT]のデータと重ねて表示して見ます。
([JT]の2本巻き線の部分は片側1本のみとしています)
赤色の●点が
[JT]のデータで 黄緑色の+点が最小2乗法[I2TC]のデータです。
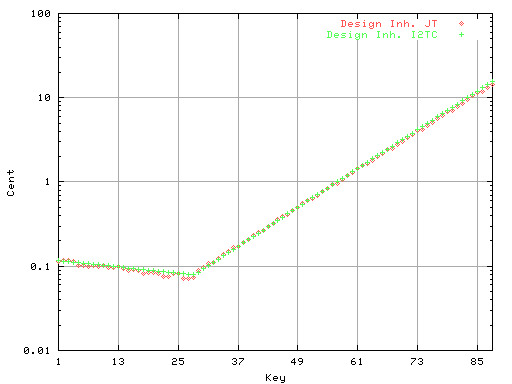 Fig.3
Fig.3
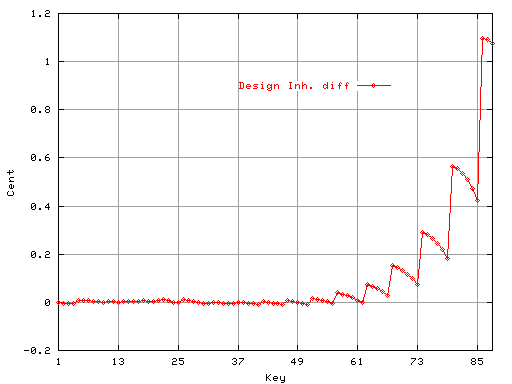 Fig.4
Fig.4
右はその差(-0.1〜1.1)の値です。
(高音部の段差は番手の差と思われます)
では Tuningをするとどうなるでしょう?
以下は [JT]でのシミュレーションです。
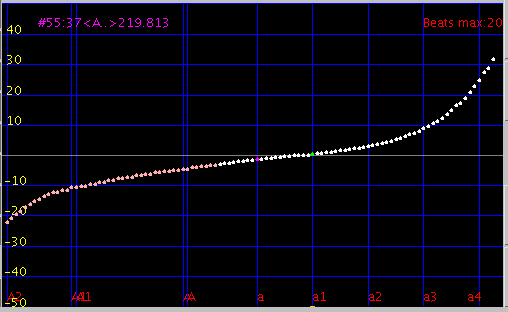 Fig.5
Fig.5
同じ条件で最小2乗法[I2TC]のインハーモニシティ値で
Tuningをした値と重ねて見ます。
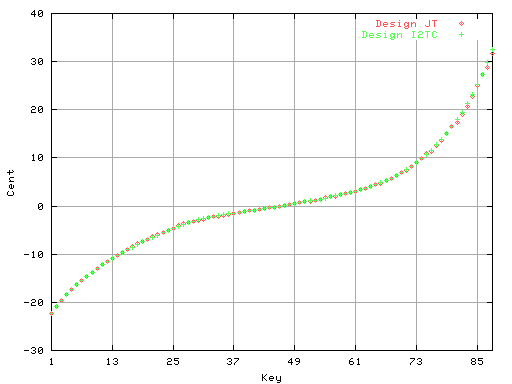 Fig.6
Fig.6
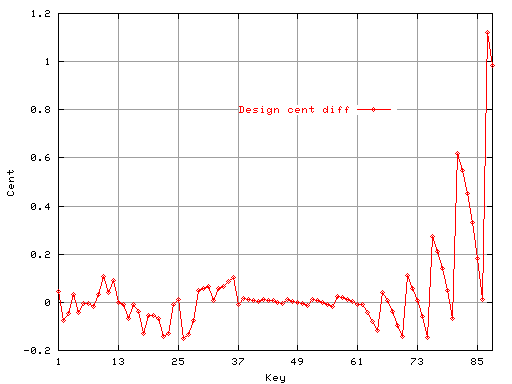 Fig.7
Fig.7
上右の図は2つの差(-0.2〜1.2[cent])の値です。
- 実際のピアノ
それでは実際のピアノではどうなるでしょう?
同じく[JT]から[sample_1]を使って見ます。
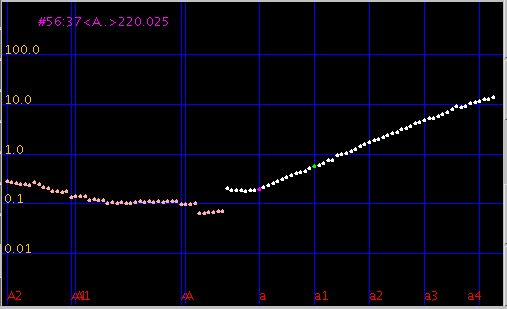 Fig.8
Fig.8
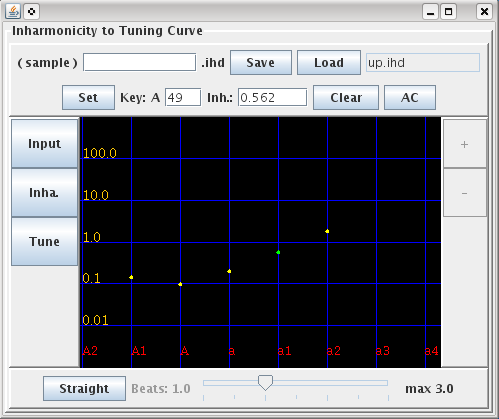
その弦データから計算したインハーモニシティ値から
5つのデータを取り出します。
| Key# | Inha. |
|---|
| 13 | 0.138 |
| 25 | 0.099 |
| 37 | 0.199 |
| 49 | 0.562 |
| 61 | 1.8 |
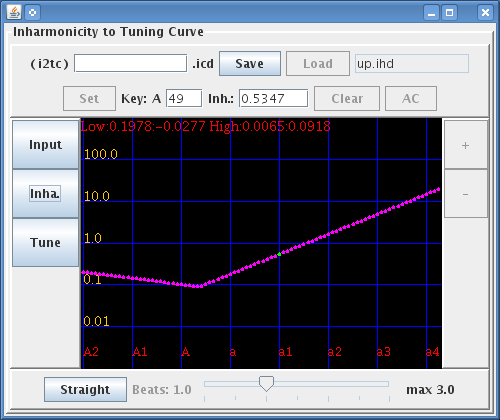
その数値を最小2乗法[I2TC]で計算した値と重ねて見ます。
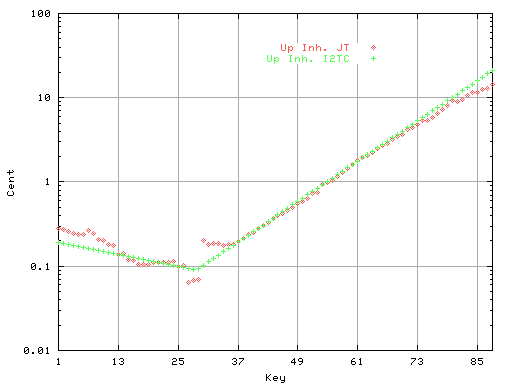 Fig.9
Fig.9
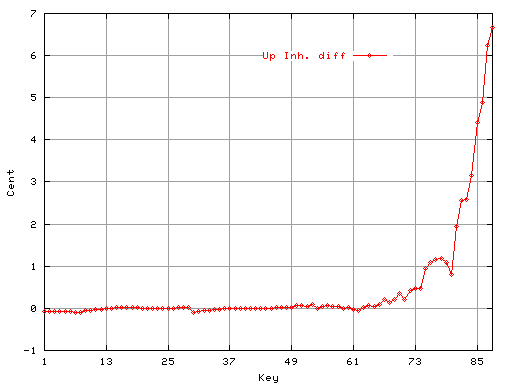 Fig.10
Fig.10
上右の図は弦データと計算値との差(-0.1〜7)です。
それからTuning(シミュレーション)をするとどうなるでしょう?
まず[JT]でのデータです。
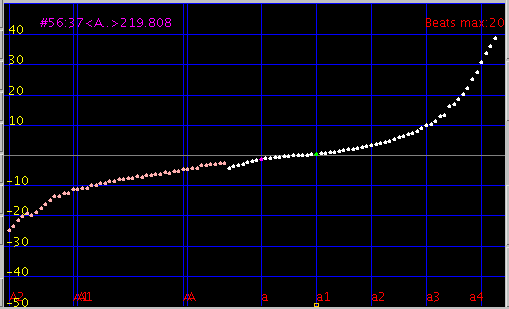 Fig.11
Fig.11
そして最小2乗法[I2TC]で計算した値と重ねて見ます。
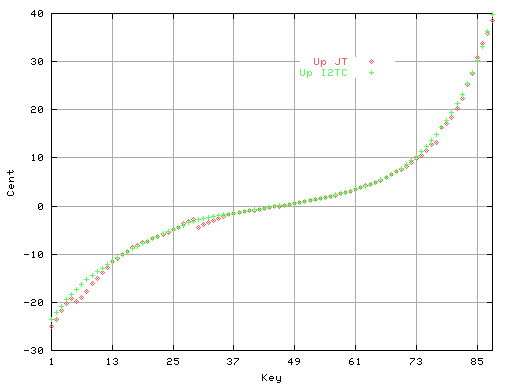 Fig.12
Fig.12
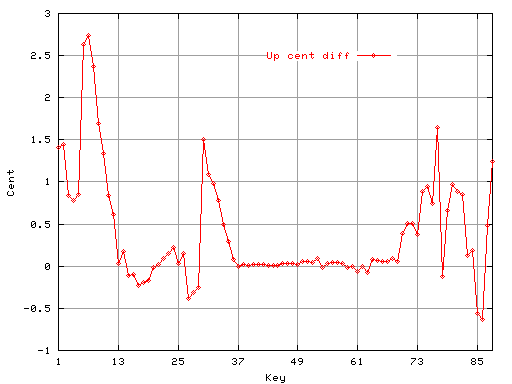 Fig.13
Fig.13
上右の図は2つのデータの差(-1〜3[cent])です。
- フォルテピアノ [Broadwood 1815]
今度は[JT]からフォルテピアノ[Broadwood 1815]で試して見ます。
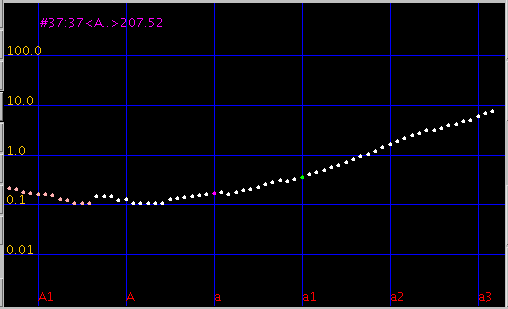 Fig.14
Fig.14
そこから5つのデータを使います。
| Key# | Inha. |
|---|
| 13 | 0.162 |
| 25 | 0.127 |
| 37 | 0.168 |
| 49 | 0.362 |
| 61 | 1.716 |
最小2乗法[I2TC]で計算した値と重ねて見ます。
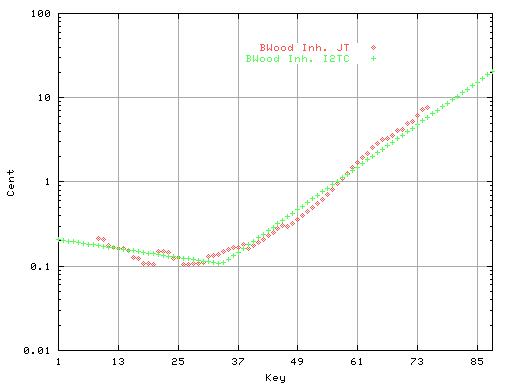 Fig.15
Fig.15
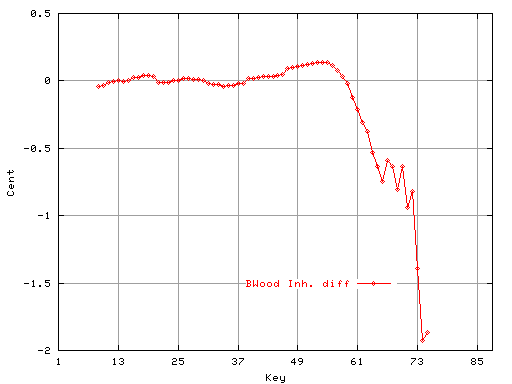 Fig.16
Fig.16
上右の図は2つのデータの差(-2〜0.2)です。
(範囲以外のデータは削除しています)
Tuning(シミュレーション)ではどうでしょう?
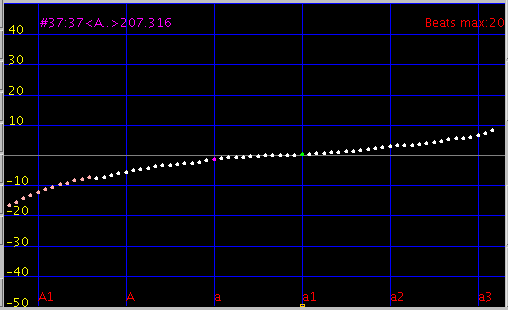 Fig.17
Fig.17
2つのデータを重ねて表示して見ます。
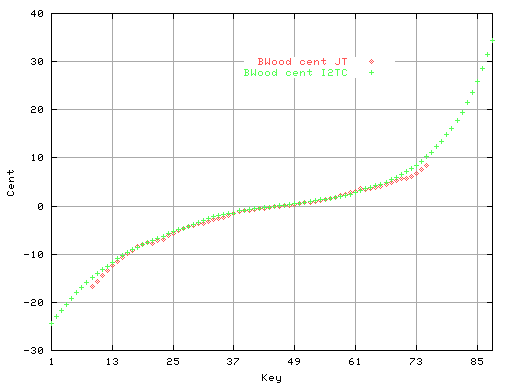 Fig.18
Fig.18
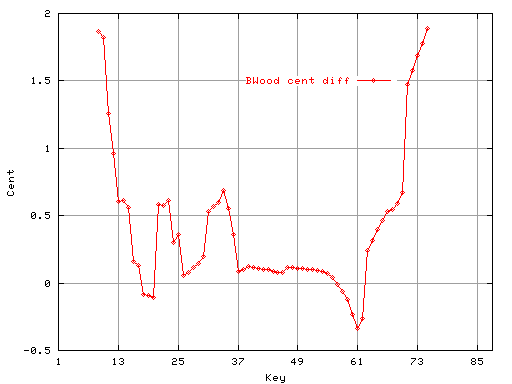 Fig.19
Fig.19
上右の図は2つのデータの差(-0.5から2)です。
(範囲以外のデータは削除しています)
その差をやはり大きいと見るか,以外と少ないと見るか...でしょうか。
java -jar i2tc.jar (もしくはクリックで起動)
Input ボタン:キー番号とインハーモニシティ値を上段の
[Key:][Inh.:]欄にキーボードから入力するか
データファイルを[Load]ボタンで選択します。
データファイルは[.ihd]の拡張子((I)n(H)armonicity (D)ataの略)で
内容は以下の様に
#は注釈行。1行目にデータの行数・変数の数,
2行目以下にキー番号・インハーモニシティ値を並べます。
# design.ihd
# key# inh.
4 2
13 0.098
25 0.083
37 0.173
49 0.499
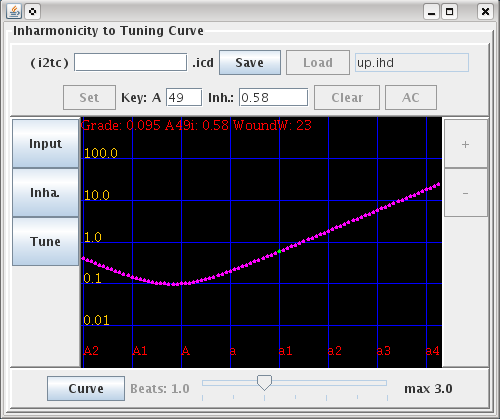
Inha(rmonicity) ボタン:インハーモニシティ値を計算します。
Tune ボタン:Tuningをシミュレーションで行います。
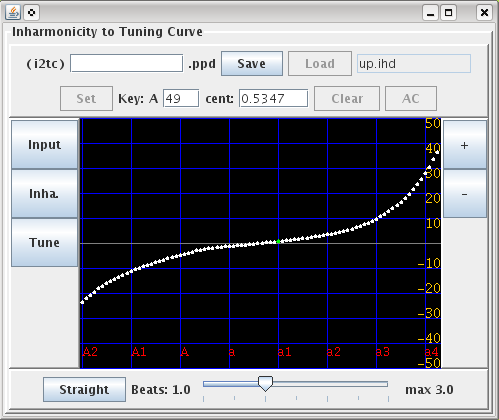
Set ボタン:[Input]の時に
[Key:]と[Inh.:]欄に入力したキー番号のデータを取り込みます。
Key [ ] テキスト欄:[Input]の時にキー番号を入力します。
Inh(armonicity) [ ] テキスト欄:[Input]の時に
インハーモニシティ値を入力します。
[Tune]の時にはセント値[cent:]を表示します。
Clear ボタン:[Input]の時に[Key:]番号の[Inh.:]データを
0にします。
A(ll)C(lear) ボタン:
[Input]のデータ全てを 0にします。
上左 (sample)[ ].ihd テキスト欄:
[Save]時ファイル名をデフォルトから変更したい時に記入します。
(拡張子は自動に追加されるので記入の必要はありません)
又 動作中に起きたエラー内容を表示します。
Save ボタン:データをファイルに書き出します。
デフォルトでは[Input]では[sample.ihd]に
[Inha.]では[i2tc.icd]に
[Tune]では[i2tc.ppd]と言うファイル名になります。
[Inha.]時に計算結果を [Low:0.1173:-0.0138 High:0.0066:0.0883]
[Low:]Bass側・[High:]芯線側として記録します。
Load ボタン:[Input]時にファイルから
データを取り込む時に使用します。
[ ] テキスト欄:[Load]したファイル名を表示します。
右側 + | - ボタン:[Tune]の時にセント値目盛の最大値を±
25, 50, 100に切替えます。
下段 Curve | Straight 切替えボタン:
インハーモニシティ値の計算と[Tune]のシミュレーションを
[Curve]曲線と[Straight]直線に切替えます。
Beats スライダー:[Tune]の時にうなりの差を
0〜3の間で変化させます。移動後再び[Tune]ボタンを押して下さい。
マウスの左クリックでカーソルの「移動/固定」を切替えます。
「移動」の時にはマウスのカーソルを動かす事で
選択キーが変更出来ます。現在位置のキーは
緑色で表示されます。
カーソル位置のキー番号・データは[Key:][Inh.:]欄に表示されます。
v0.7.1['13/02/18] Tuningのシミュレーション(TuningFormula2.java)を
catenary型に改定しました。
cssファイルを別にしました。
v0.7['08/06/08] [Curve]曲線での設計・Tuningを加えました。
v0.6['07/06/03] Tuning部分を別のクラス(TuningKeys.java)にしました。
v0.5['07/04/17] [Reset]ボタンを[Clear]に改名しました。
最小2乗法の計算用 LSM.javaを加えました。i2tc.zip掲載。etc.
v0.4.1['05/10/11]
v0.4['05/09/15] 周波数の計算方法を変更しました。
v0.3.1['05/04/29] 小修正
v0.3['05/04/13] [Tune]の計算方法を改訂しました。etc.
v0.2.2['04/12/29] 段落分け・データのテーブル表示に変更など。
v0.2.1['04/12/28] 差のグラフの±を逆にしました。
v0.2['04/11/29] [Save]時にファイル名を付けられるようにしました。
同時にボタンの位置を変更しました。
v0.1['04/11/08]
v.β['04/10/25]
v.α['04/10/09]
 Fig.2
Fig.2
 Fig.3
Fig.3
 Fig.4
Fig.4
 Fig.5
Fig.5
 Fig.6
Fig.6
 Fig.7
Fig.7
 Fig.8
Fig.8
 Fig.9
Fig.9
 Fig.10
Fig.10
 Fig.11
Fig.11
 Fig.12
Fig.12
 Fig.13
Fig.13
 Fig.14
Fig.14
 Fig.15
Fig.15
 Fig.16
Fig.16
 Fig.17
Fig.17
 Fig.18
Fig.18
 Fig.19
Fig.19
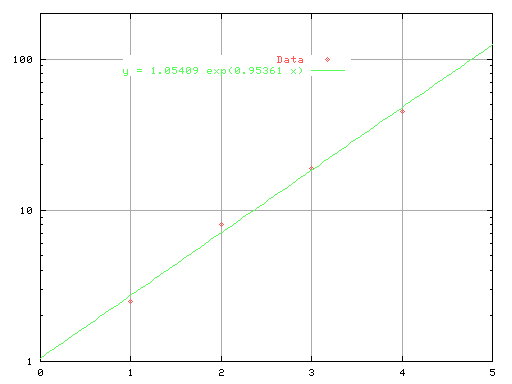 Fig.1
Fig.1
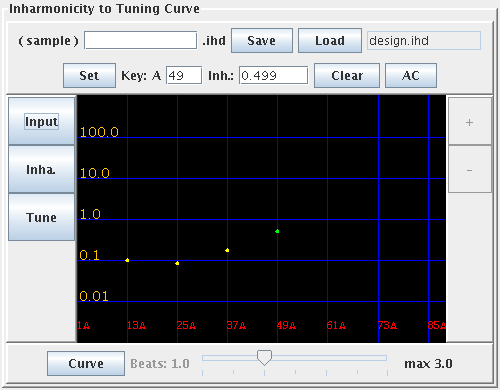 Fig.20
Fig.20



