 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
データを新たに 2つ加えて JPの測定データ(Pitch)をJavaアプレットで表示します。
例えば 以下の様な測定データを...
... 56E.. Pitch:7.303 Inharmo.:1.185 (0.969) 52C.. Pitch:5.882 Inharmo.:0.883 (0.945) 49A.. Pitch:3.793 Inharmo.:0.7 (0.925) 44E.. Pitch:5.177 Inharmo.:0.419 (0.954) 40C.. Pitch:5.282 Inharmo.:0.272 (0.98) 52C.. Pitch:5.424 Inharmo.:0.859 (0.997) ...
...「awk」を使って...
% cat ccat
#!/usr/bin/awk -f
BEGIN { FS = " " }
{ $1 = substr($1, 1, 2)
$2 = substr($2, 7)
print $1 " " $2
}
% ccat jpdata > data0
... 56 7.303 52 5.882 49 3.793 44 5.177 40 5.282 52 5.424 ...
...キーとセント値を取り出します。
キーが重複していて 順番も前後していますが そのまま読み込みます。
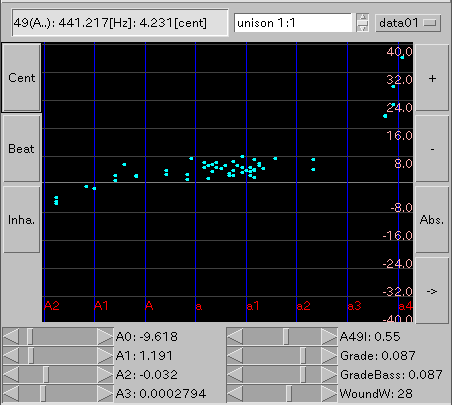
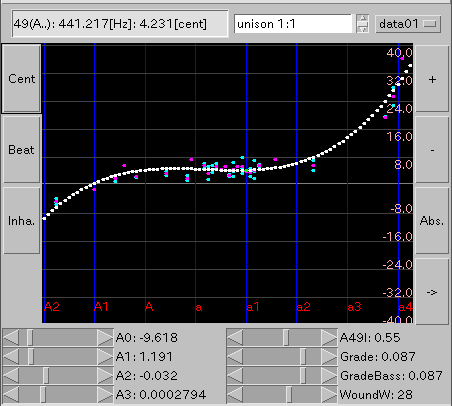
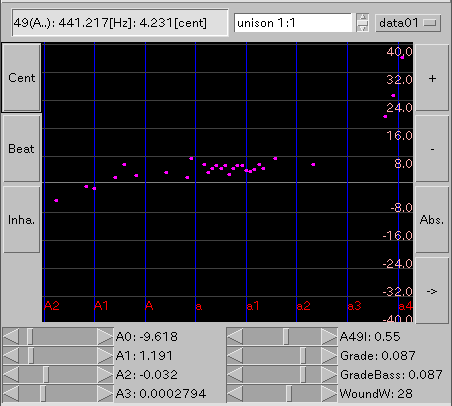
複数あるキーは 平均値を出します。
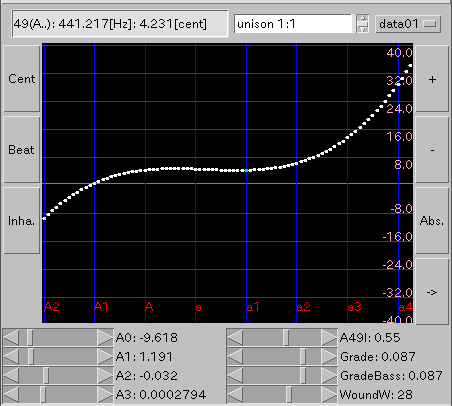
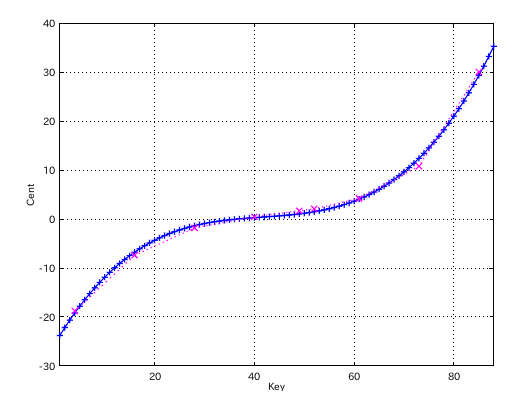
lsm(最小自乗法) 三次関数近似で 調律曲線の近似値を計算します。
全て表示します。

 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
(※変更履歴:
v0.1.8['17/11/04]
「前奏曲集 1」のデータを見直しました。
これまでのデータと相関係数を見る jcor.javaを追加しました。
v0.1.7['17/10/01]
「子供の情景」の参照CD数を11から12にしました。
新たな参照曲を加えました。
v0.1.6['17/09/04]
相関係数をTuningのシミュレーションを使って調べてみました。
v0.1.4['17/08/12]
別の曲を使って見ました。
v0.1.3['17/08/05]
相関係数を新たに調べました。
v0.1.2['17/07/30]
lsm(最小自乗法)を一部修正して値が少し変わりました。
v0.1['17/06/11])
画面左側 [ Cent ] トグルボタン:

最初は lsm3のグラフですが ボタンを繰り返し押す事で 4つの画面を順次切替えます。



[ Beat ] ボタン: 'うなり'を表示します。
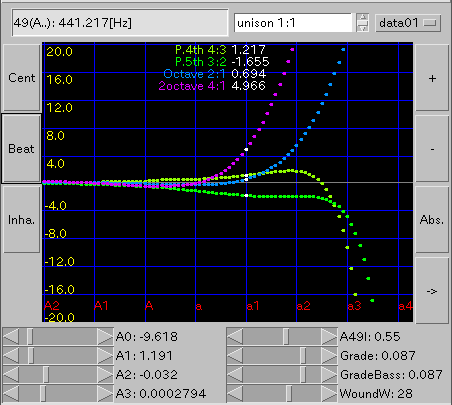
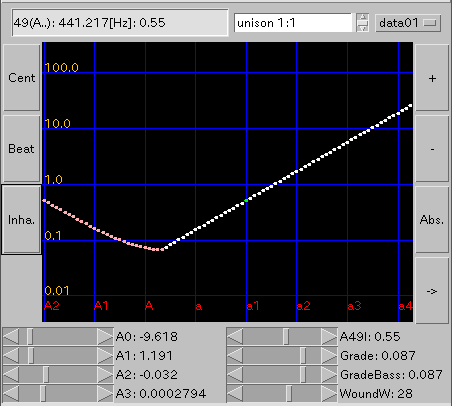
[ Inha(rmonicity) ] ボタン: インハーモニシティ値を表示します。
画面上段 [ ] テキストフィールド: カーソルの位置データを表示します。
[ unison 1:1 ... 3octave 8:1 ] セレクタ: [Beat]で表示する'うなり'を選びます。
[ data01 ... ] セレクタ: 表示するセント値のデータを選びます。
画面右側 [ + ][ - ] ボタン: [Beat][Cent]画面の上下サイズを変更します。
[ Abs(olute) ] ボタン: [Beat]画面で 'うなり'の値を絶対値で表示します。
[ -> | <- ] トグルボタン: [Beat]画面で'うなり'の方向を切替えます。
画面下段左 [ || ] A0 スライドバー: 最小自乗(lsm)3次関数の a0の値です。
[ || ] A1 スライドバー: 最小自乗(lsm)3次関数の a1の値です。
[ || ] A2 スライドバー: 最小自乗(lsm)3次関数の a2の値です。
[ || ] A3 スライドバー: 最小自乗(lsm)3次関数の a3の値です。
画面下段右 [ || ] A49I スライドバー: インハーモニシティ値の A49の値です。
[ || ] Grade スライドバー: インハーモニシティの傾き(Grade)の値です。
[ || ] GradeBass スライドバー: 巻き線のインハーモニシティの傾き(Grade)を表します。
[ || ] Wound スライドバー: 巻き線の数を表します。
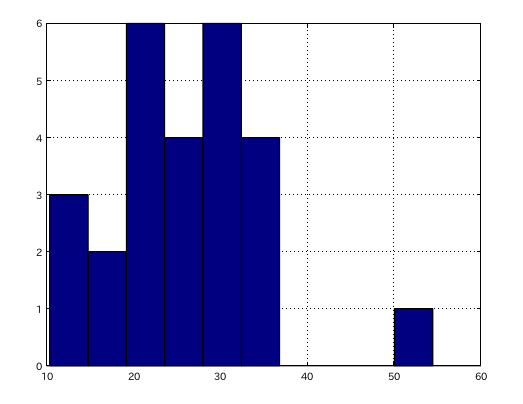
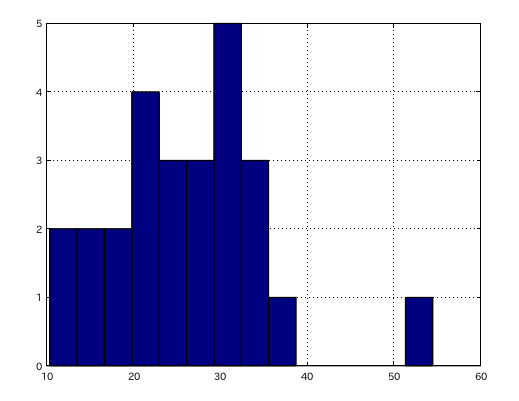
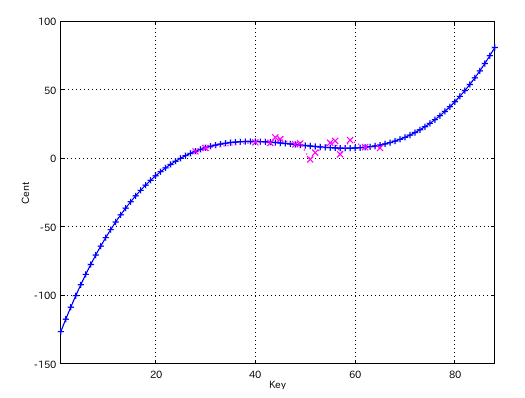
調律曲線の大きさを 今回は C88-A49のセント差で表して見ました。
C(88)-A(49) : A49Inha. : Grade ------------------------------ 29.947 : 0.6413 : 0.0973 10.341 : 0.6085 : 0.0811 21.933 : 0.5986 : 0.0833 25.866 : 0.6261 : 0.0892 19.646 : 0.5531 : 0.0844 20.292 : 0.5797 : 0.0881 30.782 : 0.6020 : 0.0892 36.782 : 0.6107 : 0.0829 13.771 : 0.5913 : 0.0820 26.496 : 0.6058 : 0.0888 23.937 : 0.5771 : 0.0808 54.475 : 0.4988 : 0.0775 26.429 : 0.4198 : 0.0756 28.719 : 0.5870 : 0.0831 22.202 : 0.6082 : 0.0897 11.89 : 0.6138 : 0.0837 23.274 : 0.6382 : 0.0931 29.582 : 0.5829 : 0.0912 31.152 : 0.6011 : 0.0870 15.417 : 0.5952 : 0.0885 21.115 : 0.6310 : 0.0921 17.897 : 0.6189 : 0.0866 35.171 : 0.5994 : 0.0887 29.697 : 0.6211 : 0.0894 32.726 : 0.6389 : 0.0910 34.293 : 0.6389 : 0.0910 ------------------------ 合計数 26
10段階のヒストグラムで表してみます。
14段階で表してみます。
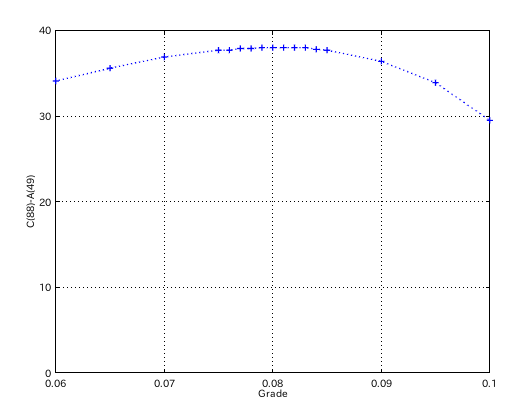
A(49)のインハーモニシティ値と 傾き(Grade)のグラフです。
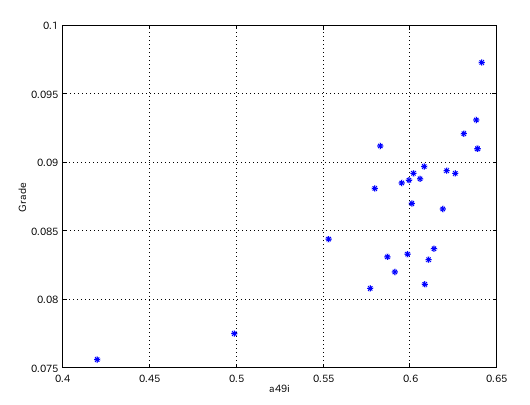
傾き(Grade)と C(88)-A(49)セント差のグラフです。
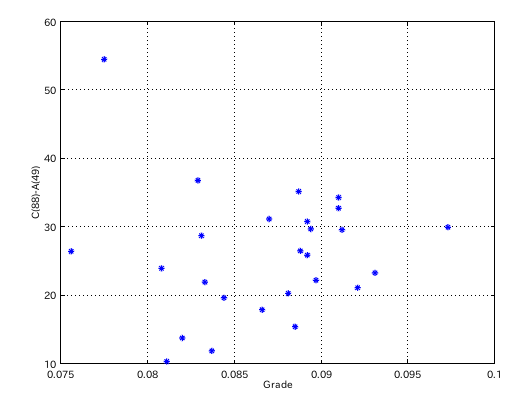
因みに相関係数は -0.0048822でした。
インハーモニシティ値と C(88)-A(49)セント差のグラフです。
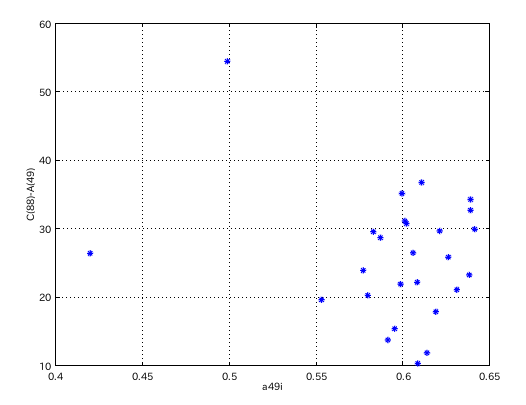
相関係数は -0.20836でした。
ただし「HTML5版 三和音調律シミュレーション (HTML5 Triads Tuning Simulation)」などでは インハーモニシティ値と C(88)-A(49)セント差は 増加する傾向で 相関係数は 0.99999ですが...
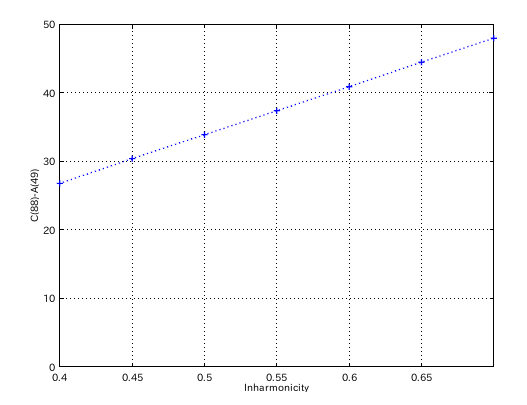
傾き(Grade)とC(88)-A(49)セント差では 0.08で最高値を示して 相関係数は -0.33736となりました。
相関係数はこれからも勉強して行きますが それでも測定値は あまりに変幻自在な様に見受けられます。
(v0.1.3)相関係数を他のキー間隔で調べて見ました。
3オクターブのセント差の場合です。
A(49)~A(85): -0.021267 A(37)~A(73): -0.18065 A(25)~A(61): -0.35731 A(13)~A(49): -0.22256 A(1)~A(37) : -0.041908
測定位置に依って 相関係数は変化します。
2オクターブです。
A(61)~A(85): 0.012131 A(49)~A(73): -0.10148 A(37)~A(61): -0.31353 A(25)~A(49): -0.32830 A(13)~A(37): -0.13859 A(1)~A(25) : -0.00035414
1オクターブです。
A(73)~: 0.037181 A(61)~: -0.037306 A(49)~: -0.22102 A(37)~: -0.3489 A(25)~: -0.25378 A(13)~: -0.062684 A(1)~ : 0.030873
3オクターブの A(25)の前後のキーを見てみます。
E(20)~: -0.33388 F(21)~: -0.34356 Fis(22)~: -0.35091 G(23)~: -0.35576 Gis(24)~: -0.35793 A(25)~: -0.35731 B(26)~: -0.35382 H(27)~: -0.34745 C(28)~: -0.33827
2オクターブの A(25)の後を見てみます。
A(25)~: -0.32830 B(26)~: -0.33721 H(27)~: -0.34446 C(28)~: -0.35003 Cis(29)~: -0.35388 D(30)~: -0.35595 Es(31)~: -0.35617 E(32)~: -0.35444 F(33)~: -0.35065 Fis(34)~: -0.34471
オクターブの A(37)の前後です。
F(33)~: -0.33868 Fis(34)~: -0.34319 G(35)~: -0.34642 Gis(36)~: -0.34834 A(37)~: -0.34890 B(38)~: -0.34801 H(39)~: -0.34556 C(40)~: -0.34141 Cis(41)~: -0.33541
A(25)3オクターブの 相関係数 -0.35731となった セント差と傾き(Grade)の グラフです。
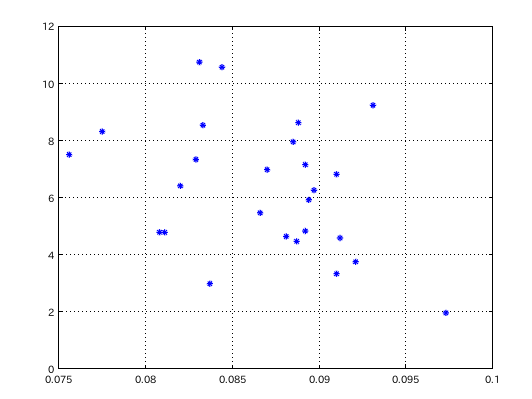
割り振りの範囲(F(33)~F(45))を含むと
相関係数が上昇する様に見えます。と言う事は
傾き(Grade)と調律曲線の大きさには
相関関係があると考えられます。
では近似値の調律曲線からではなく 測定したデータから
lsm(最小自乗法)で傾きを計算して
そのセント差と傾き(Grade)を 相関係数で見てみます。
3オクターブです。
A(1)~: -0.070118 A(13)~: -0.24812 A(25)~: -0.40303 A(37)~: -0.18078 A(49)~: -0.063804
2オクターブです。
A(1)~: -0.14290 A(13)~: -0.016198 A(25)~: -0.34022 A(37)~: -0.32356 A(49)~: 0.11472 A(61)~: 0.027625
1オクターブです。
A(13)~: (測定出来ず) A(25)~: 0.24343 A(37)~: -0.23069 A(49)~: 0.075114 A(61)~: (測定出来ず)
データの有り無しの間隔に左右されますが
相関係数はほぼ同じ傾向にあります。
では相関係数の高い値の前後です。
3オクターブです。
G(23)~: -0.28718 Gis(24)~: -0.40325 A(25)~: -0.40303 B(26)~: -0.36903
2オクターブです。
D(30)~: -0.28066 Es(31)~: -0.41590 E(32)~: -0.46783 F(33)~: -0.46463 Fis(34)~: -0.46463 G(35)~: -0.46463 Gis(36)~: -0.45802 A(37)~: -0.32356
1オクターブです。
Gis(24)~: 0.23879 A(25)~: 0.24343 B(26)~: 0.23167 ... Fis(34)~: -0.24028 G(35)~: -0.25288 Gis(36)~: -0.25641 A(37)~: -0.23069
1オクターブではデータの変化が大き過ぎて相関係数は小さく
2オクターブではデータの有り無しの影響がありますが
高い相関関係を示しています。
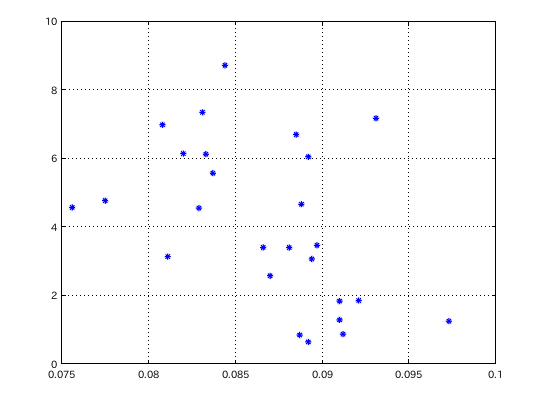
2オクターブのE(32)の 相関係数 -0.46783のグラフです。
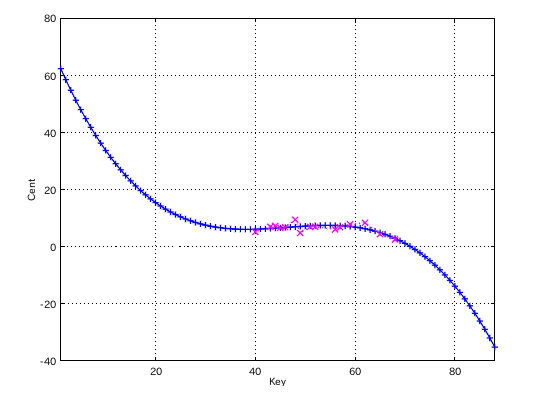
(v0.1.4)別の曲を使って見ます。
シューマンの「子供の情景」を (v0.1.7)11->12例です。
A(49)Inha. : Grade
------------------
0.5325 0.0750
0.6077 0.0767
0.6752 0.1107
0.6027 0.0973
0.5974 0.0952
0.6101 0.0957
0.6385 0.0962
0.6724 0.1087
0.6235 0.1050
0.6241 0.0930
0.6600 0.0993
0.6351 0.0927
-------------
合計 12
そのグラフを追加しました。(v0.1.7)
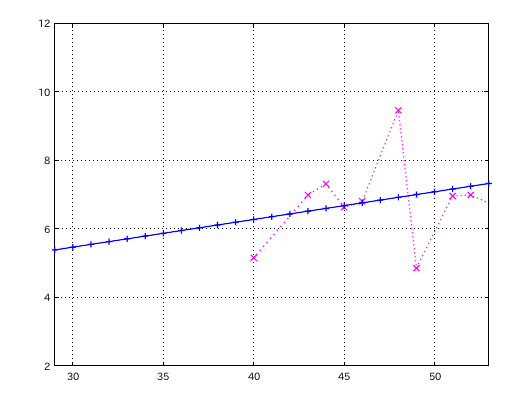
単音で B(26)ぐらいから G(71)ぐらいまでありますが その両端の音は測定が難しくデータに取り上げられない場合があります。
出来ても範囲が十分ではなく 最小自乗法(lsm)3次関数では 正常な調律曲線は再現出来ませんでした。
しかし相関関係を 2オクターブ(直線最小自乗法)で見ると
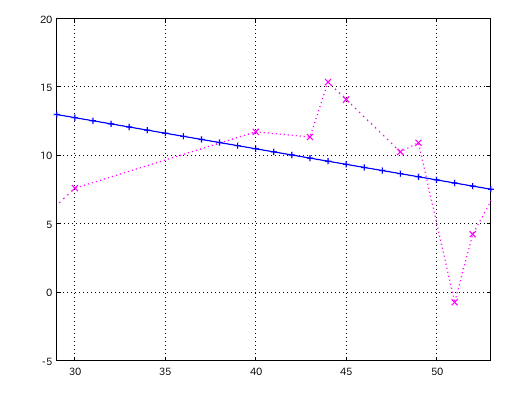
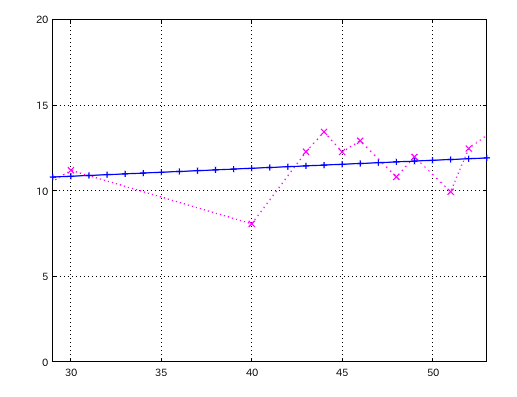
A(61)~: (測定出来ず) A(49)~: 0.097928 A(37)~: -0.51543 A(25)~: -0.54771 A(13)~: (測定出来ず)
A(25)前後を見てみます。
Gis(36)~: -0.56531 G(35)~: -0.56531 Fis(34)~: -0.53283 F(33)~: -0.53283 E(32)~: -0.53233 Es(31)~: -0.64699 D(30)~: -0.79884 Cis(29)~: -0.80188 C(28)~: -0.76857 H(27)~: -0.70101 B(26)~: -0.58242 A(25)~: -0.54771 Gis(24)~: -0.40787
Cis(29)の2オクターブで 相関係数 -0.80188と言う 音程差と傾き(Grade)の関係を見る事が出来ます。
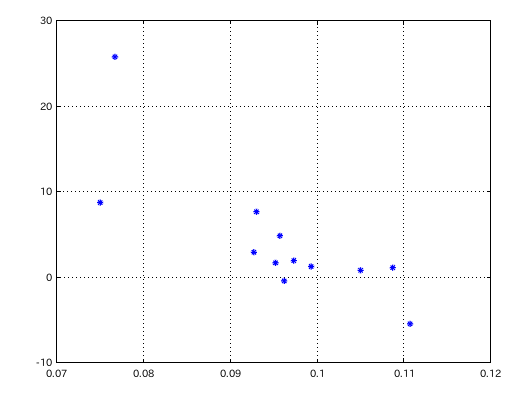
(v0.1.6)Tuningのシミュレーションの場合です。
0.05から0.1まで 0.005づつ 傾き(Grade)を変えて
作った調律曲線をデータにして 相関係数を測定しました。
「TuneTriads(三和音)」2オクターブでの 音程差と傾き(Grade)の相関係数です。
A(61)~: 0.015514 A(49)~: -0.94494 A(37)~: -0.99833 A(25)~: -0.98946 A(13)~: -0.98769 A(1)~ : -0.98997
37(A)から2オクターブの相関係数 -0.99833のグラフです。
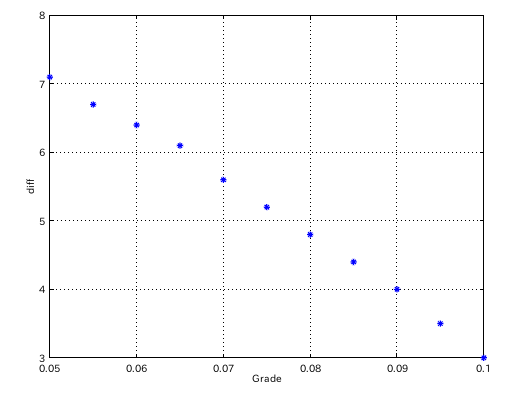
49(A)以下ではほとんど変化しません。 それをグラフにして見てみます。
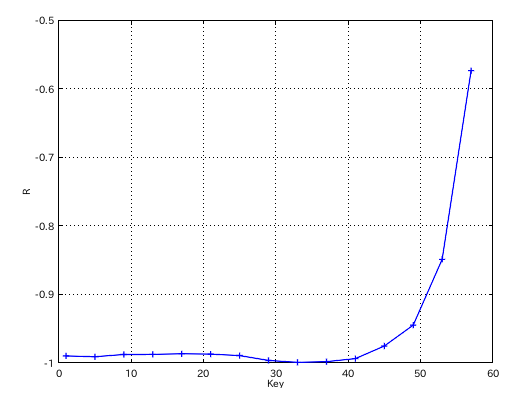
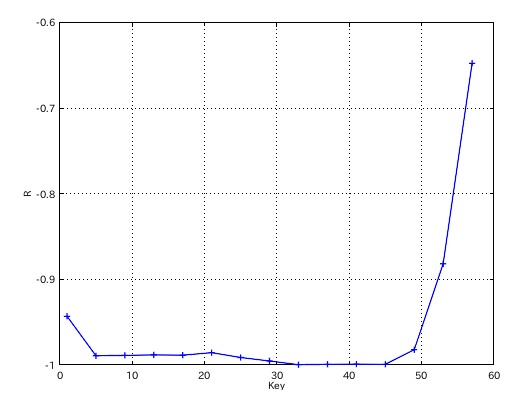
他のTuningシミュレーションで見てみます。
「NonZero」と「Octave」の場合です。
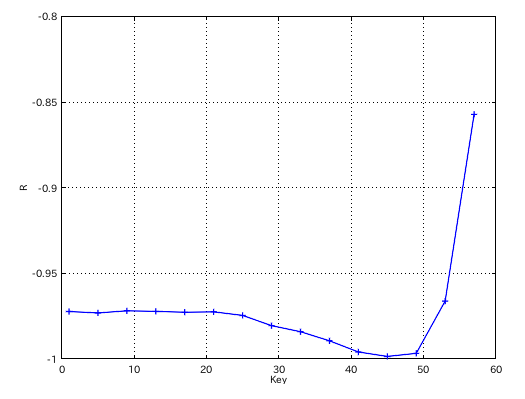
「Curve」の場合は低音で異なりますが他は殆んど同じです。
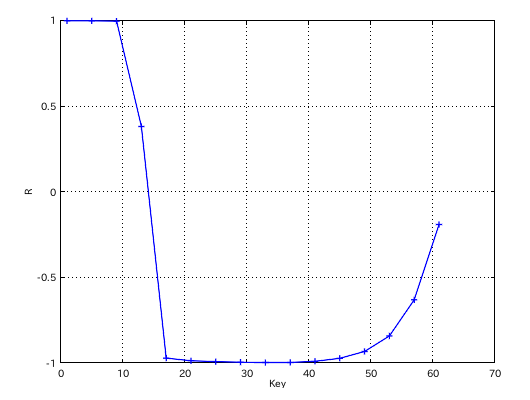
因みに「前奏曲集 1」と「子供の情景」 2オクターブでの相関係数のグラフです。
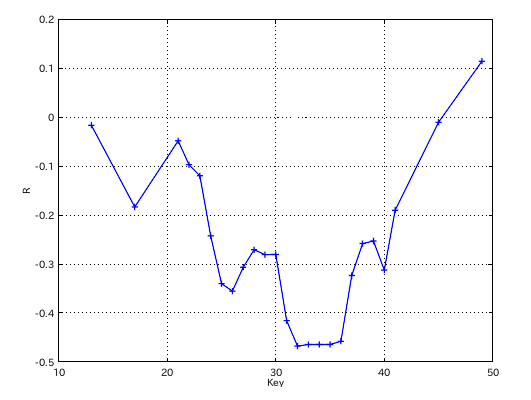
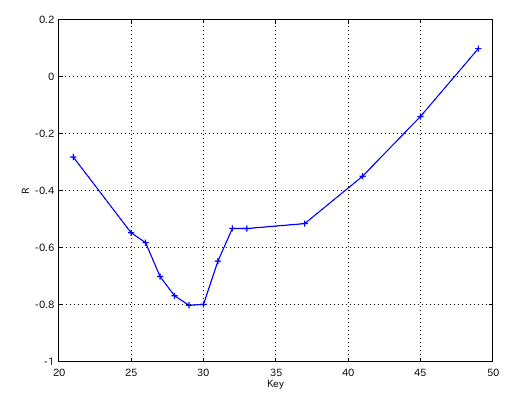
49(A)以下で 2オクターブ以上の範囲のデータが ある程度集まれば 相関係数は 測定出来ると思われます。
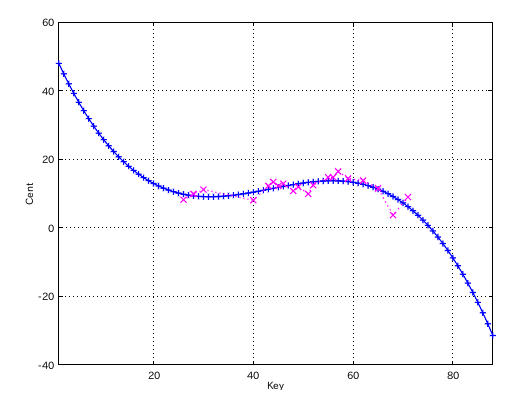
(v0.1.7)例に ショパンの「4つのバラード」(CD16種類)で D(30)ぐらいから C(52)前後までを検出して 見てみます。
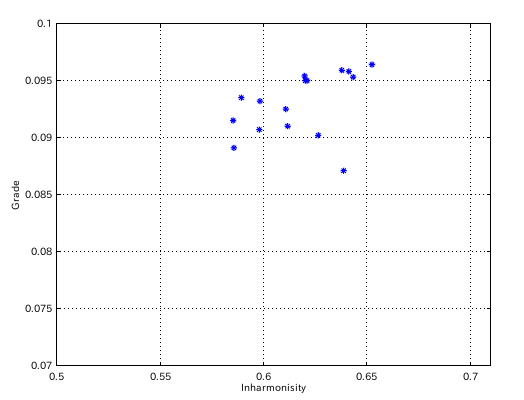
#. A(49)インハーモニシティ値 : 傾き(Grade) ------------------------------------------ 1. 0.6117 : 0.0910 2. 0.6199 : 0.0954 3. 0.5980 : 0.0907 4. 0.5983 : 0.0932 5. 0.6108 : 0.0925 6. 0.5853 : 0.0915 7. 0.5857 : 0.0891 8. 0.5893 : 0.0935 9. 0.6265 : 0.0902 10. 0.6202 : 0.0950 11. 0.6525 : 0.0964 12. 0.6413 : 0.0958 13. 0.6434 : 0.0953 14. 0.6211 : 0.0950 15. 0.6379 : 0.0959 16. 0.6388 : 0.0871 -------------------
そのグラフです。
2オクターヴでの相関係数のグラフです。
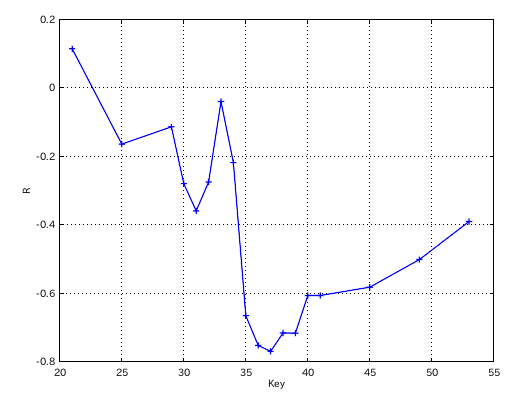
A(37)キーでの音程差と傾き(Grade)の相関係数 -0.76942です。
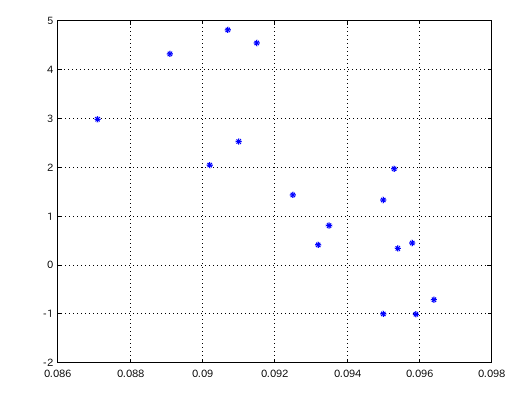
そのデータを集めていた途中での事です。
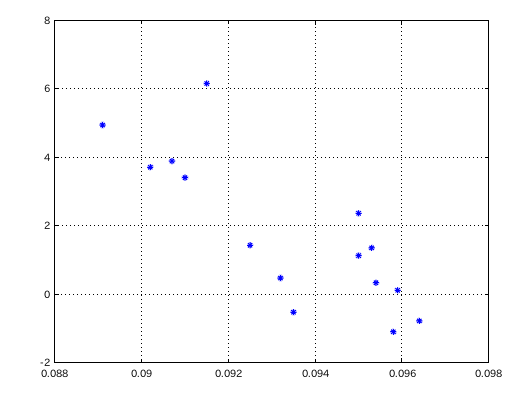
傾き(?)が 2つある様に見えます。そこでデータを 2つに分けて見ました。
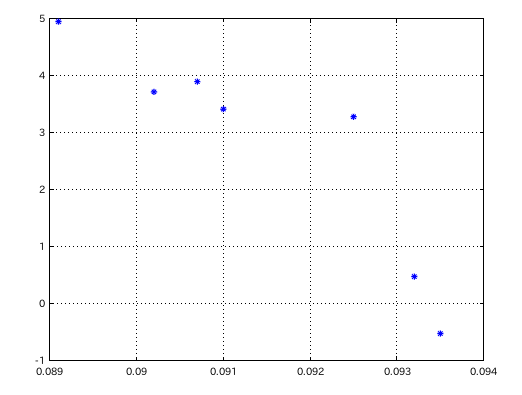
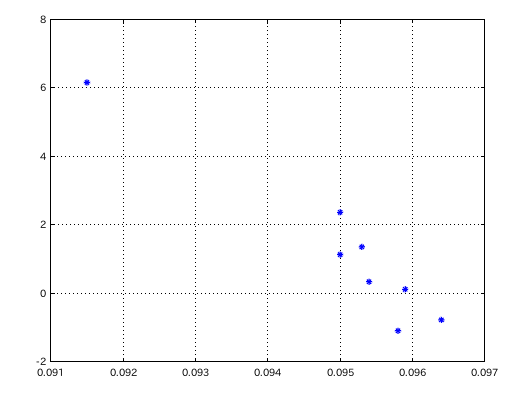
その相関係数は -0.90137と -0.95698です。
(v0.1.8)「前奏曲集 1」のデータを厳密に見直して
新しく 1つ (1と2からの選集で「アナカプリの丘」が無いのですが
これまでから 高音キーのデータは無くてもいいので) 加えました。
(26 -> 27)
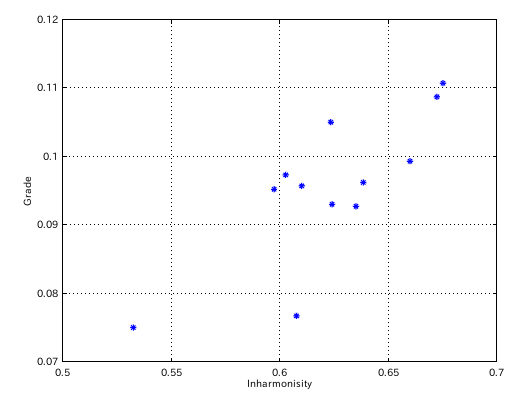
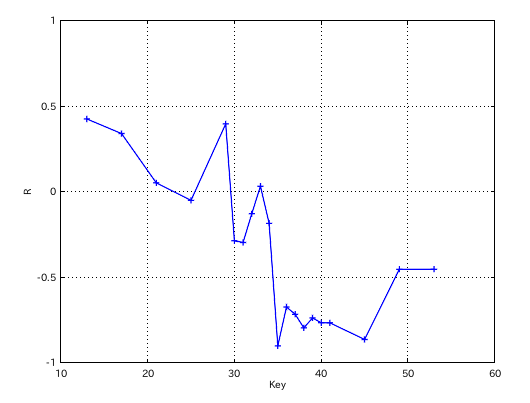
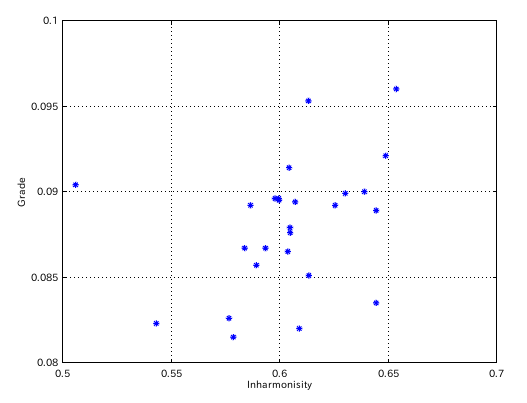
インハーモニシティ値と傾き(Grade)のグラフです。
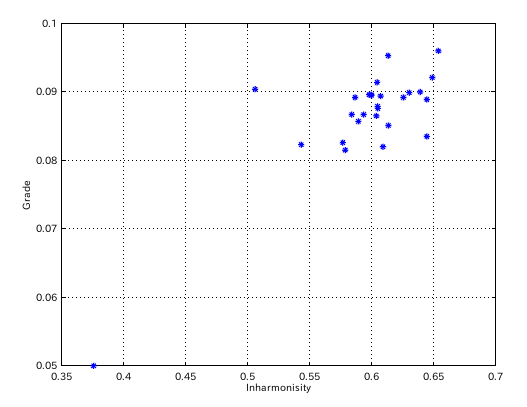
極端に異なった左下のデータを 1つ削除して結局 (27 -> )26に戻りました。
# : A(49)インハーモニシティ値 : 傾き(Grade) ------------------------------------------- 01: 0.6444 : 0.0889 02: 0.6048 : 0.0876 03: 0.5934 : 0.0867 04: 0.6255 : 0.0892 05: 0.6537 : 0.0960 06: 0.5431 : 0.0823 07: 0.5838 : 0.0867 08: 0.5892 : 0.0857 09: 0.6090 : 0.0820 10: 0.6047 : 0.0879 11: 0.6043 : 0.0914 12: 0.5766 : 0.0826 13: 0.5059 : 0.0904 14: 0.5786 : 0.0815 15: 0.5995 : 0.0896 16: 0.6071 : 0.0894 17: 0.6444 : 0.0835 18: 0.5865 : 0.0892 19: 0.5978 : 0.0896 20: 0.6037 : 0.0865 21: 0.6302 : 0.0899 22: 0.6393 : 0.0900 23: 0.6488 : 0.0921 24: 0.6134 : 0.0851 25: 0.5997 : 0.0895 26: 0.6132 : 0.0953 -------------------
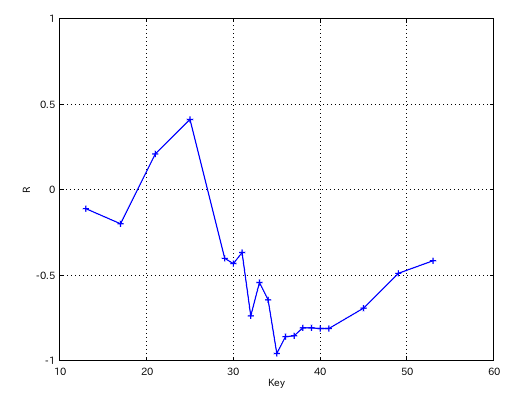
そのグラフです
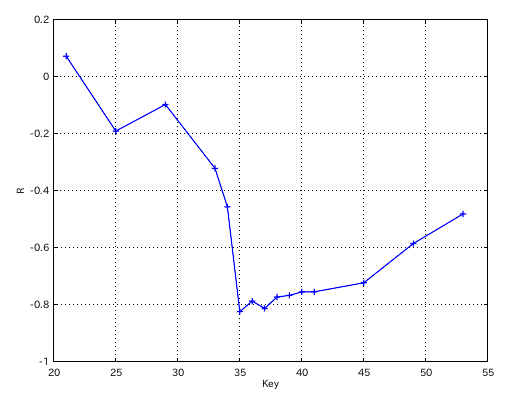
2オクターヴでの相関係数のグラフです。
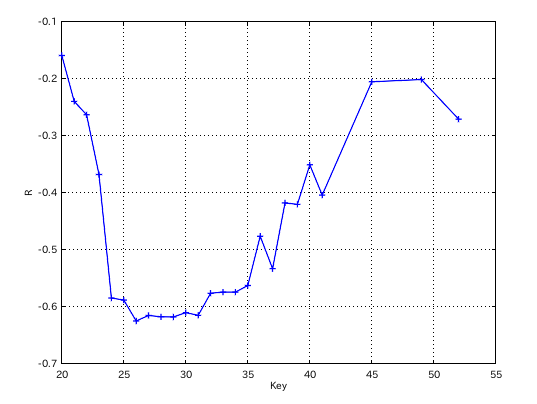
B(26)キーでの音程差と傾き(Grade)の相関係数は -0.62495です。
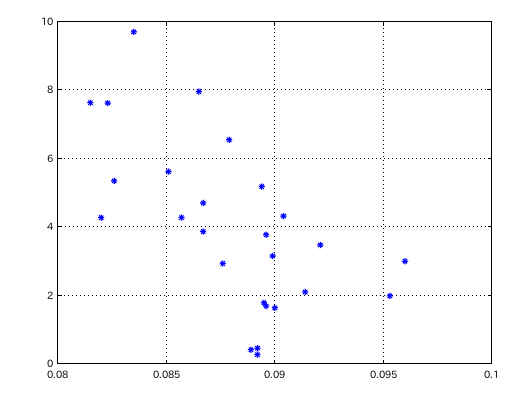
データの数が多くても これぐらいまでになりました。
実際の調律と傾き(Grade)の関係を見てみようと
ずいぶん遠回りをしてしまいました。
まだまだ分からない事はありますが
ある程度は描けた様に思いますが いかがでしょうか。
(v0.1.8)jcor.javaアプレットで これまでのデータと相関係数を見てみます。
jlデータ内の極端な測定値を 2〜3箇所削除しましたが 他は殆んど前と同じです。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
(※変更履歴:
v0.1.1['18/04/08] HTML5版
相関係数(Correlation 5 XHR)を追加しました。
v0.1['17/11/04] )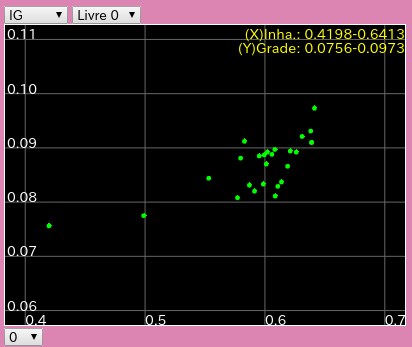
HTML5版です。
画面左 [ Cent ] トグルボタン:
今回は lsm(最小自乗法)を表示しません。 元のデータと その平均値のみを ボタンのクリックで切替えます。
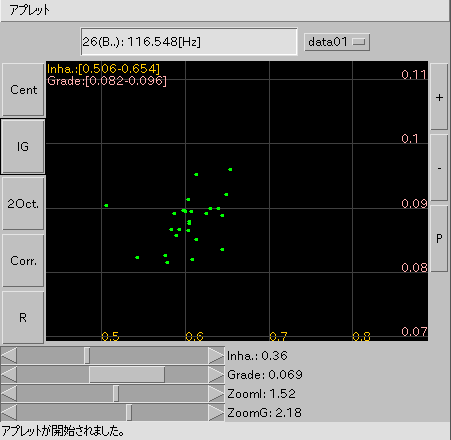
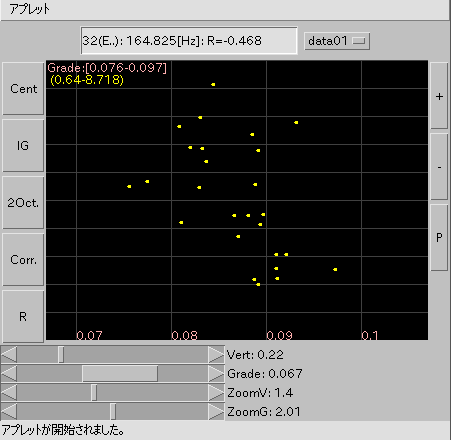
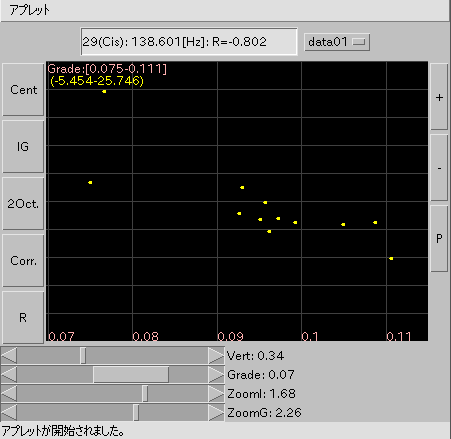
[ IG ] ボタン: インハーモニシティ値と傾き(Grade)を表示します。
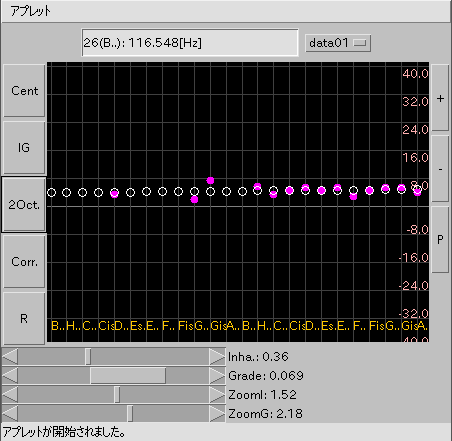
[ 2Oct(ave) ] ボタン: 2オクターブ分のデータ(ピンク色)と その lsm(最小自乗法)(白枠丸)を表示します。 (計算が出来ない場合は lsm値は上端に表示されます。)
[ Corr(elation) ] ボタン: キー 1〜88までの 2オクターブでの相関係数を表示します。 計算出来ない時は NaNとして 赤く画面上端に表示されます。
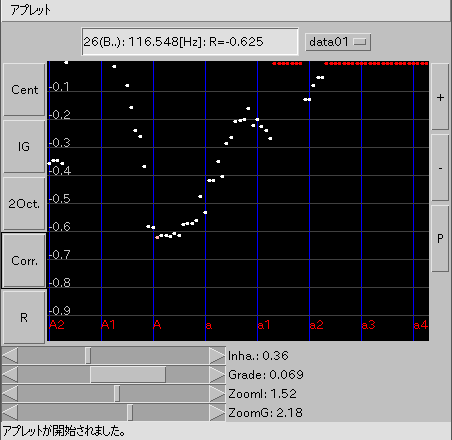
[ R ] ボタン: そのキーでの 2オクターブの相関係数を表示します。

画面右 [ + ][ - 」ボタン: [Cent][2Oct]画面で上下幅を増減します。
[ P(olarity) ] ボタン: [Corr]画面で 表示を マイナスデータのみとプラスとマイナスの 両方かを切替えます。
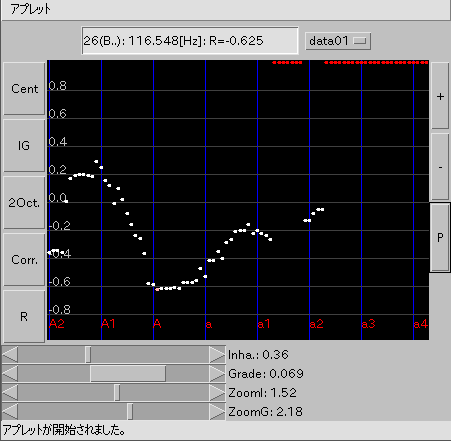
画面下 [ Vert: 0.4 ] スライダー: [IG]表示の時は Inha(rmonisity)で左右の位置を(0.1)調整します。 [R]表示の時は 上下の位置を調整します。
[ Grade: 0.08 ] スライダー: [IG]表示では 上下の位置を(0.03)調整します。 [R]表示では 左右の位置を調整します。
[ ZoomV: 2.0 ] スライダー: [IG]表示の時は左右で [R]表示では上下を 2倍まで拡大します。
[ ZoomG: 2.0 ] スライダー: [IG]表示の時は Gradeの上下を [R]表示の時は Gradeの左右を 3倍まで拡大します。
画面上 [ 26(B..): 116.548[Hz]: R=-0.625 ] テキスト表示: [Cent][IG][2Oct]では カーソル位置の キー名と周波数のみで [Corr.][R]では 上記と相関係数を R=-0.625 などと表示します。 (計算出来ない時は NaN(Not a number)と表示されます。)
[ data01 ] セレクター: 1つずつのデータを選択します。
最初の「前奏曲集 1」です。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
「子供の情景」です。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
「TuneTriads(三和音)」でのTuningシミュレーションです。
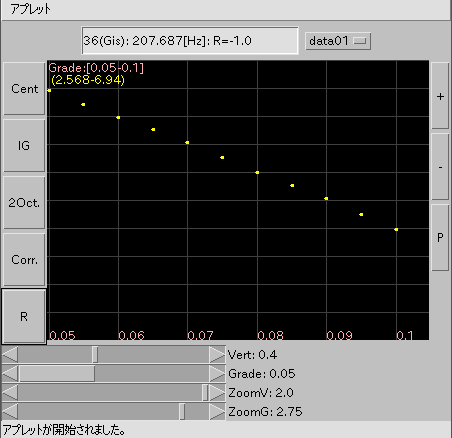 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
「4つのバラード」です。
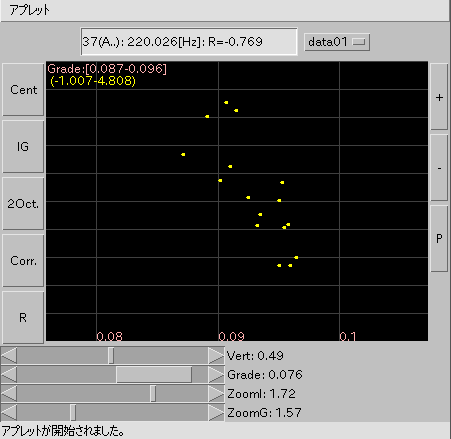 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
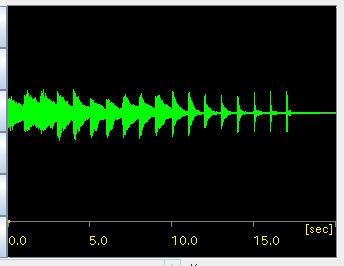
参考までに JPのキャリブレーション用に 楽譜作成プログラム(LilyPond)で作成したMIDIファイルを...

...MIDI再生プログラム(Timidity++)で Wave信号に変換して見てみます。
最小自乗法です。
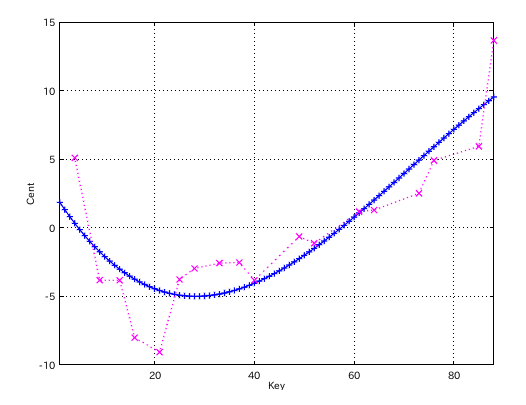
低音が上がっていますので削除して再計算しました。
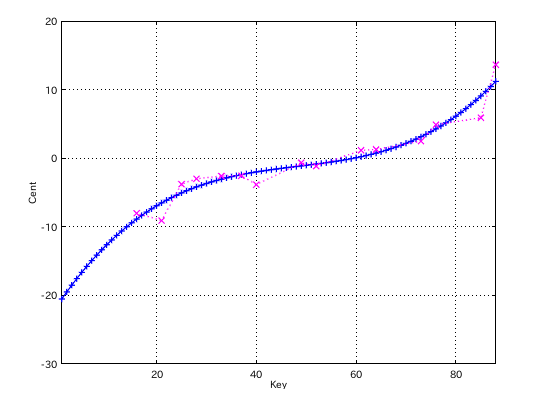
数値計算プログラム(Octave)で Wave信号を
合成して見てみます。
インハーモニシティ値です。
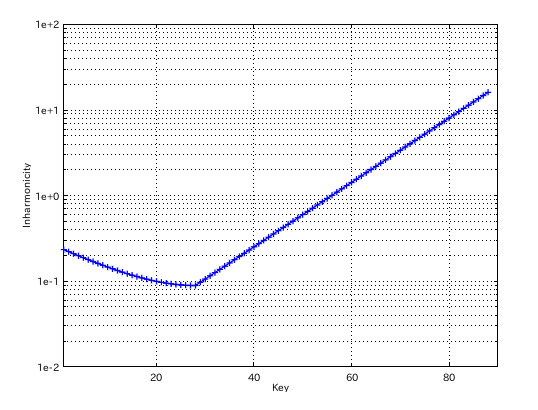
三和音式で Tuningを行います。
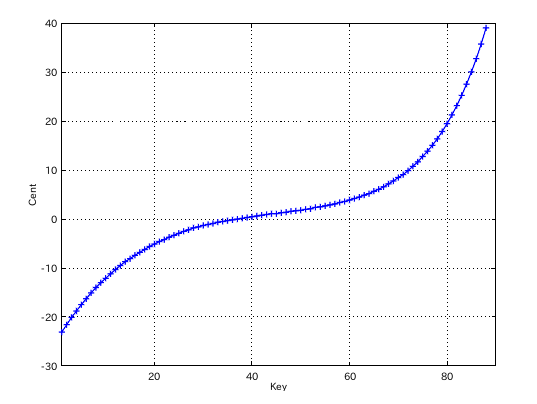
キー毎に Wave信号を作って見てみます。
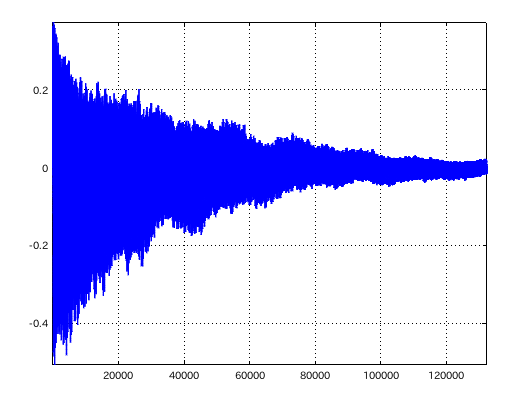
最小自乗法です。
「da-mid」「da-osc」としてセレクタに加えました。