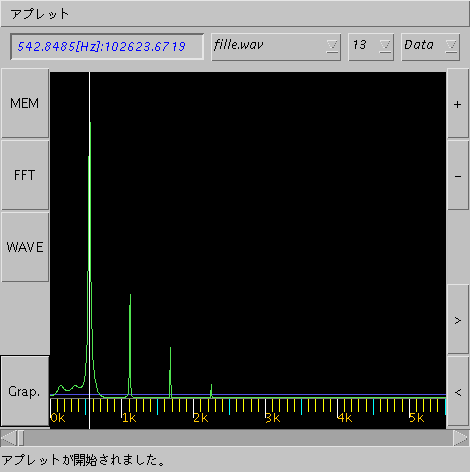
有限な測定データからそれだけでは測定不可能な大きなラグを持つ 自己相関関数を情報エントロピーが最大となるように推定することにより スペクトル推定を行う。
したがって 無限に続く信号(現象)の一部分だけからスペクトル解析をす るのに適している。
FFTと比較すると スペクトルの分解能が高い・ 信号の周期に対してデータ長が短くてもスペクトル推定が出来る・ 雑音に対して比較的強い etc.
MEMの使用上の注意点としては 自己回帰モデルの次数決定が難しい最終予測誤差 (FPE:Final Prediction Error)を用いているが どのデータでもこの方法がうまく行くとは限らない・ スペクトルの推定結果は和とはならない(高さは保証されない)・ FFTに比べ計算時間が長い etc.
![]() (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
(※ 変更履歴:
v1.6.5['19/10/27] HTML5版を追加しました。
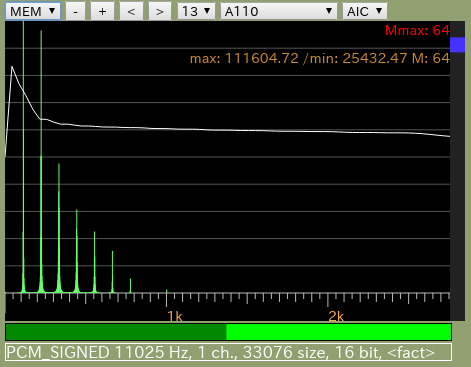
HTML5版です。
v1.6.4['13/02/26] [Wave]の表示など少し変更しました。
v1.6.3['12/12/03] cssファイルを別にしました。
データの表示を見やすく整えました。
v1.6.2['12/11/11]
ReadWave.javaのmonoとStereoの切替えの不具合を訂正しました。
v1.6.1['07/11/29] ReadWave.java(v0.2)に修正しました。
v1.6['07/10/21] Burg法[参考文献: 2]を取り入れた
MemBurg.javaを別クラスにしました。
FFTをJPの精度に変更しました。Mmaxの設定ボタン類を無くしました。
v1.5['05/9/10] Waveファイルの読み込み部分を別クラスにしました。
v1.4['05/8/31] FFTを変更しました。
周波数の計算方法を変更しました。
v1.3['04/03/24]
S・M・LでJava画面のサイズを変更出来るようにしました。
v1.2 Waveファイルの読み込み部分を変更しました。
ステレオはモノラルにして測定します。
一部のOSでFFTのグラフが表示されなかったのを修正しました。
v1.1「<> / ><」ボタン位置を変更しました。
「G / T」ボタンの表示を逆にしました。)
画面上:左から テキストフィールド: データやエラー情報を表示します。
[ a49-4-8.wav ] Wave音声ファイルを選びます。
[ 11 ] 信号のサンプル数を選びます。
「 Data | G | C | FPE | AIC 」
[Data]では MEM | FFT での解析結果をみます。
以下は MEMでの計算結果です。
[ G ] は 予測誤差フィルター値です。
[ C ] は 自己相関係数です。
[ FPE ] は 予測誤差の分散です。
[ AIC ] は 赤池情報基準です。
画面左上から[ MEM ] Burg法のMEMで信号を解析します。
Mmaxは 2√N(データ数)に固定しています。
Mmaxが最適値より大きくなると MEMは双峰を持った贋のスペクトル形
を与えます[参考文献: 2]ので、その時はサンプリング数を少なく
してみて下さい。
[ FFT ] FFTで信号を解析します。(JPのコードを利用しました。)
[ Wave ] Wave信号をみます。 下のスラーダで選択範囲を選びます。
「Grap. / Text」 グラフィック画面またはピーク値のテキストデータ画面を切替えます。
画面右上から「+ | −」グラフ画面で信号の高さを増減します。 (信号の高さは自動的に最大値をMaxとして表示しています)
「 > | < 」 表示する最大周波数を2倍 | 1/2倍にします。
画面下段のスライドバーはテキストデータで表示されるピーク値
に制限を設けます。
制限値は滑らかに変化するように 変更しました。
[Text]画面で「peak>69265.00」の様に制限値を表示し
ています。
[Wave]では画面表示の範囲を表して
信号の解析範囲を変更します。
画面上でマウスの動きに対して垂直線のカーソルが移動します。
カーソルの固定/移動の切替えには 左ボタンをクリックします。
左上の窓にカーソル位置の周波数[Hz]とパワースペクトルのレベル
(又は データ番号とデータ値)を表示します。
より正確な値は [Text]画面で確認して下さい。
FFTについて2〜3:
FFTの周波数分解能は 例えばサンプリング周波数 10[KHz]の信号を
サンプルデータ数 512で求めると
10000 / 512 = 19.53[Hz]
44.1[KHz] を 1024で求めると
44100 / 1024 = 43.067[Hz]となります。
そこで今回のFFTは分解能を棒グラフの幅で表しています。
(v1.6)FFTはJPの精度に改めました。
これまでのWaveデータをMEMなどで見てみます。
View Wave Files
JP の"A49のインハーモニシティの無い10倍音"(a49-10.wav) の音を見てみます。
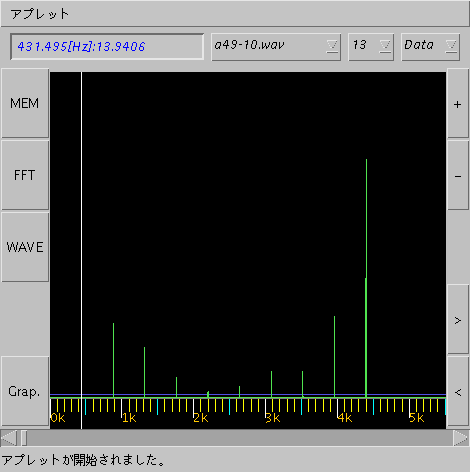
#: [Hz] Key#: [cent]: peak>1552.00: # (補正値): [cent] ------------------------------------------------ ----------------- 1: 440.0848 49A..: 0.3338: 155266.2969: 328 (0.00): 0.3338 2: 880.1697 61A..: 0.3338: 25231.1445: 655 (0.00): 0.3338 3: 1320.2545 68E..: 2.2888: 16979.0391: 982 (-1.955): 0.3338 4: 1760.3394 73A..: 0.3338: 6847.5273: 1309 (0.00): 0.3338 5: 2200.4243 77Cis: -13.3525: 2314.8914: 1636 (13.6863): 0.3338 6: 2639.1631 80E..: 1.4062: 3930.302: 1962 (-1.9550): -0.5488 7: 3079.248 83G..: -31.5968: 8899.3828: 2289 (31.1741): -0.4227 8: 3519.333 85A..: -0.3281: 9035.4619: 2616 (0.00): -0.3281 9: 3959.4177 87H..: 3.6554: 27561.0898: 2943 (-3.91): -0.2546 10: 4399.5024 89Cis: -13.882: 80788.8516: 3270 (13.6863): -0.1957
同じデータを FFTで見てみます。
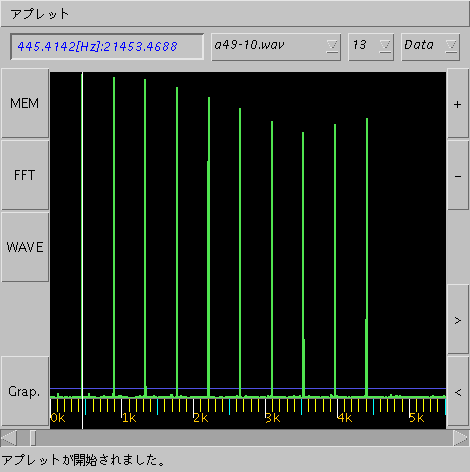
#: [Hz] Key#: [cent]: peak>51729.00: # (補正値): [cent] ------------------------------------------------- ----------------- 1: 440.0235 49A..: 0.0924: 1705369.50: 327 (0.00): 0.0924 2: 880.0255 61A..: 0.05: 1698497.375: 654 (0.00): 0.0500 3: 1320.0254 68E..: 1.9884: 1703984.125: 981 (-1.955): 0.0334 4: 1760.0405 73A..: 0.0399: 1686381.00: 1308 (0.00): 0.0399 5: 2200.0356 77Cis -13.6583: 1669221.75: 1635 (13.6863): 0.0280 6: 2640.0498 80E..: 1.9877: 1643419.75: 1962 (-1.955): 0.0327 7: 3080.0491 83G..: -31.1465: 1619719.125: 2289 (31.1741): 0.0276 8: 3520.0007 85A..: 0.0003: 1642082.50: 2615 (0.00): 0.0003 9: 3960.0029 87H..: 3.9113: 1628588.875: 2942 (-3.91): 0.0013 10: 4400.0049 89Cis: -13.6843: 1607044.625: 3269 (13.6863): 0.0020
信号音のサンプリング周波数を変更しなくても それなりの精度で測定出来ます。