 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
「振動と波動」の「1.振動」にもう一つ質量を加えた場合の振動を シミュレーションして見ました。
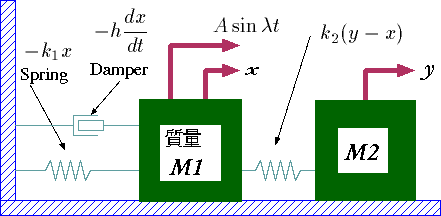
質量 M1にバネで質量 M2を繋げて M1に外力(A sinλt)を加えた時の xと yの変移を求めます。
係数としては M1 = M2 = 1, h = 3として k1, k2, A,
λは可変出来ます。
外力の「L(Rad.)」を少しずつ変化させて見て下さい。
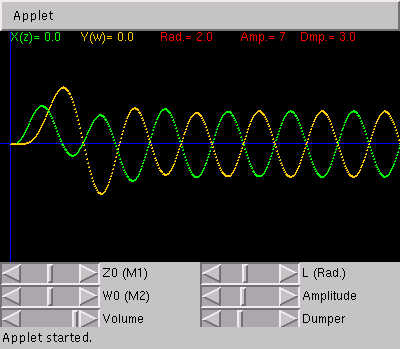
K1・K2 が 2の時 λ = 1では M1と M2は同相で λ = 2では 逆相で振動しています。
λ = √2(1.4142…)の時には M1に振動を加えているにもかかわらず M1は止まり M2のみ大きく振動を続けます。M2が M1の振動を吸収しています。
λ = √2は √(K2/M2)の事で, M2と K2の固有振動数です。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
Z0(M1):xの初期速度を変えます。
W0(M2):yの初期速度を変えます。
L(Rad.):外力の振動数をラジアン単位 (λ = 180°/ π)で変えます。
Amplitude:外力の振幅(A)を変えます。
Volume:画面の波形の大きさを調整します。
Dumper:ダンパー(k1・k2)の値を変えます。
グラフでは xの振動を緑色で yの振動をオレンジ色で表しています。
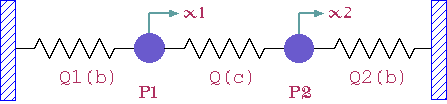
おもりP1・P2とバネQ1・Q2はそれぞれ等しく,
P1・P2の質量はm,
Q1・Q2のバネ定数はb,
中央のバネQのバネ定数をcとします。
(二本の弦が駒を通じて連結している場合とでも言えるでしょうか?)
どちらかのおもり または両方を横方向に引いてから放すと
運動が起きます。
その時の おもりP1の運動方程式は
同様にして おもりP2の運動方程式は
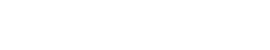
となります。
その二つの式からx1とx2を解く連立常微分方程式の経過は省略して
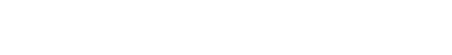
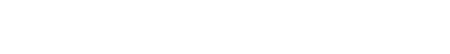
となります。またその場合
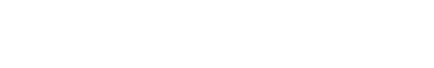
二つのおもりが同じ方向に動く場合(モード1)と
二つのおもりが逆方向に動く場合(モード2)とがあります。
[連結振動 2]の初期設定では下記の 1.の状態にしてあります。
Qc = 1・Qb = 2〜4で
P1か P2のどちらかに変位を与えると
その振動のエネルギーがもう一方に移り「共振現象」を起こします。
しかしその合成値は一定で変化しません。
(GPでソフトペダルで打鍵した場合でしょうか?)
P1とP2に同じ変位を与え
右下の極性ボタンで一方をマイナス(逆相)にすると
その合成値はゼロになります。
(整音作業で言えば ハンマーが弦を同時に打たない場合でしょうか?)
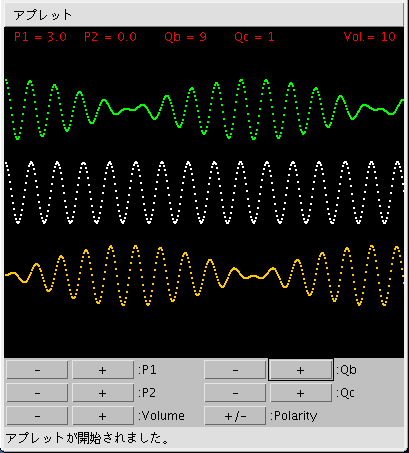 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
使い方:
P1:P2:で おもりの初期変位を変えます。
Qb:で左右のばねの係数値を Qc:で中央のばねの係数値を変えます。
Polarity:P2の位相を反転します。
Volume:画面の波形の大きさを調整します。
グラフで上の緑の線は P1の位置の変化量を, 下のオレンジの線は P2の位置の変化量を, そして中央の白色の線はP1とP2の合成値です。
(変更履歴:
v0.2.2 ['15/07/18] テキスト表示を少し変更しました。
v0.2.1 ['14/06/09] HTML5版を追加しました。
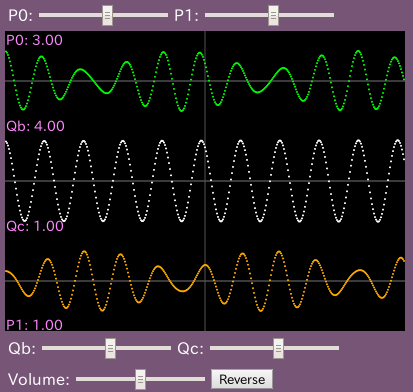
HTML5版です。
v0.2 ['12/02/16] Coupledで中央の色をシアンから白に変更しました。 Sindo2.javaとCoupled.javaを見直しました。 JavaScriptとStyleSheetを分離しました。)