ウェーヴレット序奏 (Wavelet Introduction) v1.5.3
ウェーヴレットとは 局所的に周期的な信号を時間の変化のなかで捉える
時間周波数解析の方法のひとつで、連続ウェーヴレット変換
CWT (Continuous Wavelet Transform)と離散ウェーヴレット変換
DWT (Discrete Wavelet Transform)などがあります。
(それ以上の説明は専門書やインターネットを参考にして見て下さい;)
その離散ウェーヴレット変換 (DWT)のJavaプログラム FWT
(Fast Wavelet Transform)が出来ましたので
ピアノの音などを見てみます。
(以下 左の「WAV」ボタンでは waveファイルが再生されます。
そしてJWVで見た FFT(フーリエ変換)の図と
その右にwavelet変換(FWT)の図です)
スイープ信号 (Sweep)
 (22KB)
(22KB)
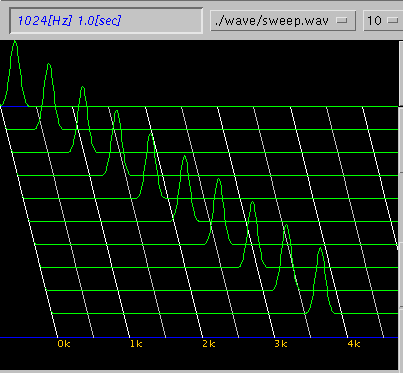
初めに 周波数が連続して変化するスイープ信号です。
1〜の段階(Jもしくは Octave)で
その周波数の高さをオクターブ毎に表します。
スパイクで音の大きさを表しています。
Wavelet変換は FFTのように周波数を特定するものではありませんが
その連続的な変化をある程度捉えています。
A(49) 440[Hz]
 (33KB)
(33KB)
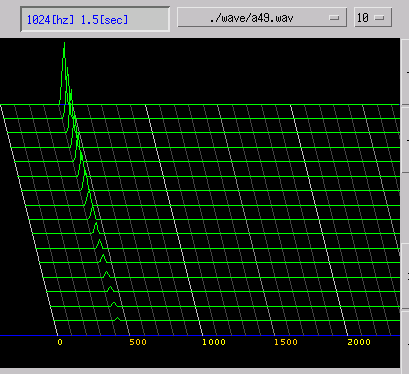
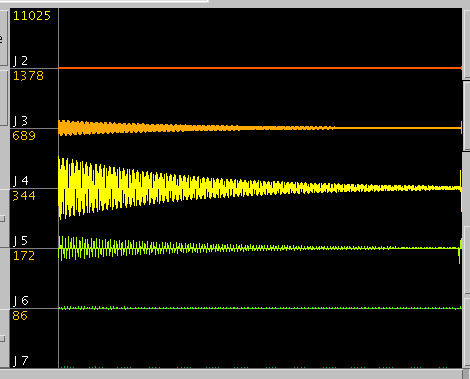
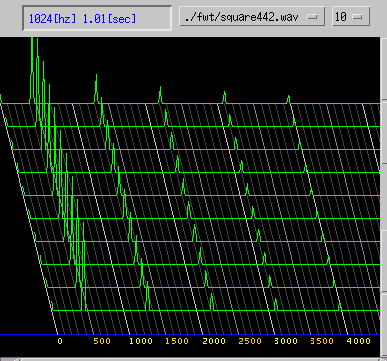
周波数の一定した音は連続したスパイクで表されます。
矩形波 (square) 442[Hz]
 (22KB)
(22KB)
パルス信号 (Pulse)
 (22KB)
(22KB)
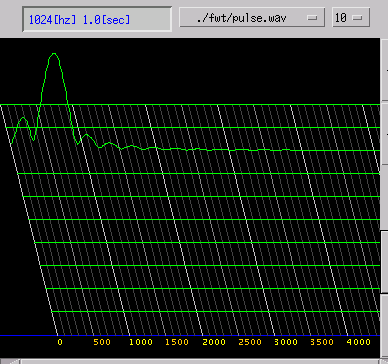
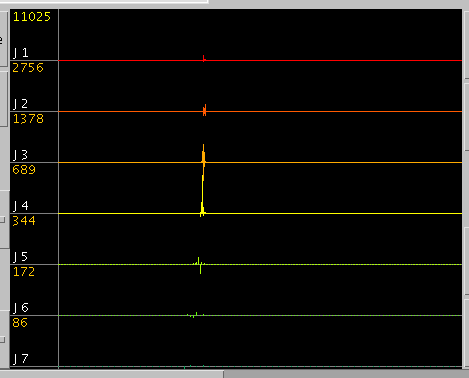
Wavelet変換ではそのパルス性をよく捉えています。
サイン波とパルス (Sine wave & Pulse)
 (22KB)
(22KB)
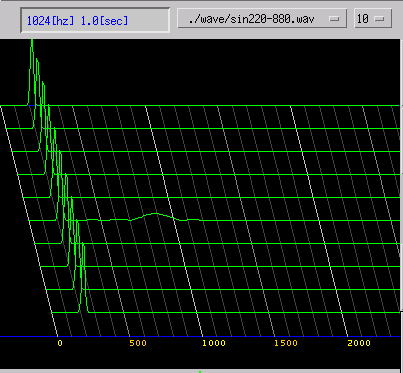
サイン波に 2サイクルのパルス信号が加わった信号です。
よく分離して認識されます。
そうした性質から 音声信号の雑音を取り除く為に利用されたりします。
下のボタンを押すと離散ウェーヴレット変換の
Javaアプレットが動作します。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
〔項目内容〕
- sweep.wav : Sweep wave
- a49.wav : A(49) 440[Hz]
- square.wav : Square 442[Hz]
- pules.wav : Pules
- sine-pulse.wav : Sine wave & pules
- hototogisu.wav : ホトトギス(鳴き声)
使い方:
- (※変更履歴:
v1.5.3['19/02/16] HTML5版を追加しました。
 HTML5版です。
HTML5版です。
v1.5.2['12/12/08] cssを分離しました。
v1.5.1['12/11/11]
ReasWave.javaのmonoとStereoの切替えの不具合を訂正しました。
v1.5['10/12/09] [Wave]と[FWT]の表示を
分けて表示するようにしました。
Waveletの表示範囲をボタンからセレクターに変更しました。
v1.4.1['07/11/29] ReadWave.java(v0.2)に修正しました。
v1.4['05/9/10] Waveファイルの読み込み(クラス)を別にしました。
v1.3['04/2/21] S・M・LでJava画面のサイズを変更出来るようになりました。
v1.2 ボタン形状一部変更
v1.1 ボタン形状・配置・スライダー動作など変更)
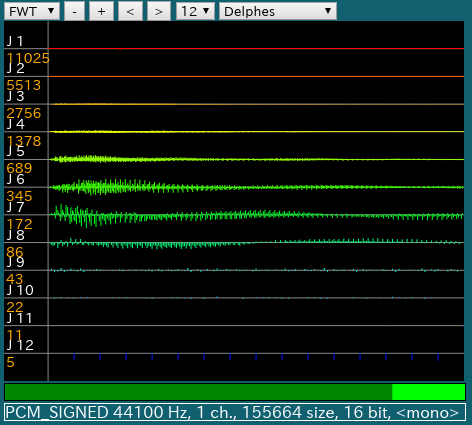
上中 [ sweep.wav ]セレクタ:Waveファイルを選択します。
上右 [ Daubechies-4 ]セレクタ:
マザーウェーヴレットの種類を選びます。
末尾の数値が大きいほど周波数の分解能が上がります。
(カッコ付きの(Symlet-#)などは プログラムの演算値未確認ですので、
参考記録として見て下さい)
上左 (※)テキストエリアには
[Wave]では Waveファイルの サンプリング周波数・時間[dec]・
〈ファイルのタイプ〉を表示します。
[FWT]では 音声信号の表示されている範囲の[%]と
(データ数/全データ数)を表示しています。
下中 スライダー:表示する信号波形の位置を調整します。
その右「Source/Wavelet」トグルボタン
(削除しました。)
右側「> | <」ボタン:表示する信号波形の幅を増減します。
「- | +」ボタン:信号波形の振幅を増減します。
(元の信号波形は変化しません)
左横 上から「∧」(Up)「∨」(Down)
削除して Start:[ 1 ]セレクターに変更しました。
表示する段階(Jもしくは Octave)の始まりを上下します。
「>=<」(Narrow)「<=>」(Wide)
削除して Wide:[ 2 ]セレクターに変更しました。
表示する段階の幅を増減します。
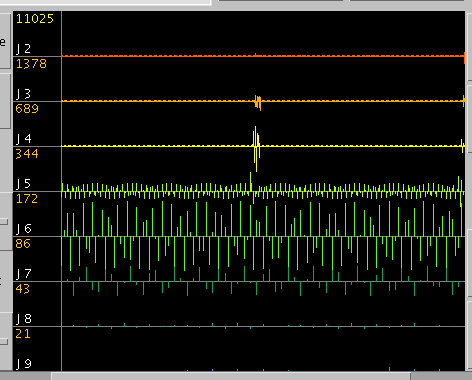
表示画面の左上には選択したwaveファイルのサンプリング周波数を
黄色で表示しています。
その下には その段階数を白色で
それの表す周波数をオレンジ色で
表示します。
これまでのWave信号を離散ウェーヴレット変換(FWT)などで見てみます。
View Wave Files
参照>連続ウェーヴレット変換
(Continuous Wavelet Transform)
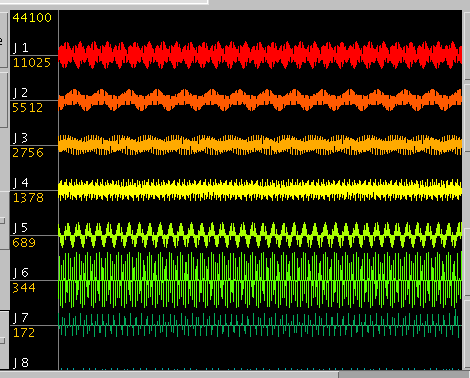
参考までに周波数発信器(サンプリング周波数 (※)44100[Hz]に固定)とした
離散ウェーヴレット変換を見て見ます。
 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
使い方:
(※変更履歴:
v1.6['10/12/09] 画面構成を FWTに合わせました。
v1.5['05/08/31] 周波数の計算方法を変更しました。
v1.4['04/02/16] 周波数の変更ボタンをキーで行う様に変更しました。)
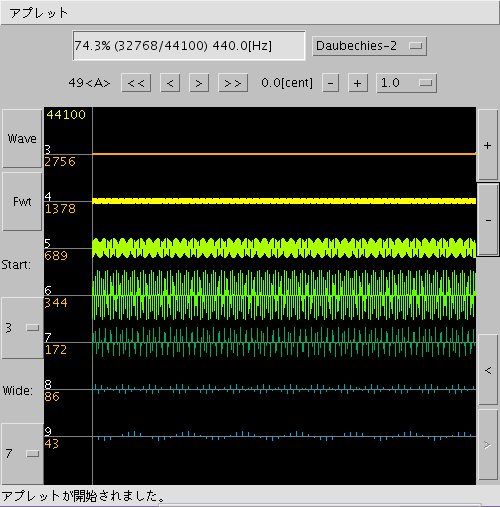
「<< | < | > | >>」ボタン:
周波数を オクターブ/1 キーずつ増減します。
「 - | + 」ボタン:キーのセント値を右の値で増減します。
「 1.0 ] セレクタ:上で変化する量を変更します。
(0.001〜50.0[cent])
(※)テキストエリアに
[Wave]では Waveファイルの サンプリング周波数・時間[dec]を表示します。
[FWT]では 音声信号の表示されている範囲の[%]と
(データ数/全データ数)・キーの周波数[Hz]を表示しています。
- その他は「FWT」と同じです。
例えば JWV(Java Wave Viewer)
での「Fille.wav」を見て見ます。
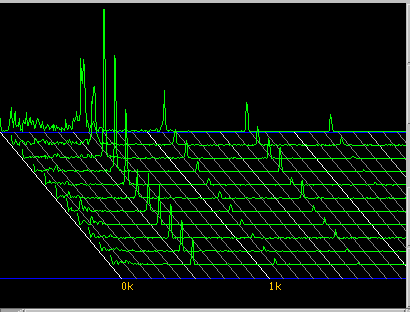 Fig-1
Fig-1
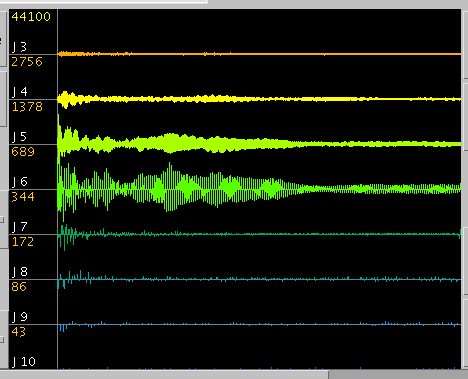 Fig-2
Fig-2
FFT(Fig-1)では基音が途中から増加するようにも見えましたが
Wavelet変換 (Fig-2)では打鍵時にも十分ある様に検出されます。
ピアノの打鍵音にはもっと多くの倍音が含まれていると思っていました。
しかしウェーヴレット変換でも特に多い様には見受けられません。
専門書などでの測定機器では 高い倍音まで出ているので
このような条件での測定では十分でないのかも知れませんが、
ピアノ以外のギター・ハープ・マリンバなどでは高い倍音が出ています。
そこから こうした音声信号からでもピアノらしい音が聞こえるのは、
その中にピアノの音の基本が含まれているからで ピアノの音の特徴は
その叩く(打鍵)という発音方法と、インハーモニシティと言う
独特の倍音構成にある様に思われます。
参照>振動と波動
(Oscillation and Wave) 3.弦の振動
参照>インハーモニシティについて
(Inharmonicity)
さて これまで御覧のように 弦の振動・楽音信号の波形・フーリエ変換・
ウェーヴレット変換・インハーモニシティのある倍音のうなりの図・
音階のグラフ・五度圏図 など様々な音の見方がありますが
ピアノのTuningやVoicingで そうした音形のイメージを思い描きながら行うのも
一つの方法かも知れません。
参考文献:
- ウェーヴレットビギナーズガイド 榊原 進 東京電機大学出版局 1995
- ウェーヴレットによる信号処理と画像処理
中野 宏毅・山本 鎭男・吉田 靖夫 共立出版 1999
- ウェーヴレット解析の基礎理論 新井 康平 森北出版 2000
Dobashi.M
Last modified: 4月 26日 金 16:04:49 2024 JST











 (Java appletは 利用出来なくなりました;)
(Java appletは 利用出来なくなりました;)
 Fig-1
Fig-1
 Fig-2
Fig-2