「アップライト 及び グランドピアノの構成」ヘルベルト・ユングハンス
"Der Piano-und Flugelbau" Junghans
の本に「駒圧力の計算」があります。
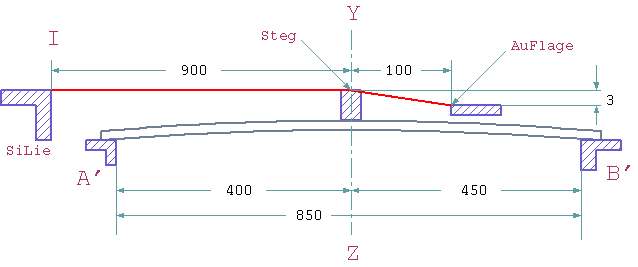 (図版177)
(図版177)
そこでは 駒とヒッチピンプレートの高さの差を 3mm・駒の長さを 135mm・ 弦の加重は5音で それぞれ3本の弦が 70Kg としています。
つまり 3 x 5 = 15本で x 70 = 1050Kg
一音では 6.3Kg・一弦では 2.1Kgと算出しています。
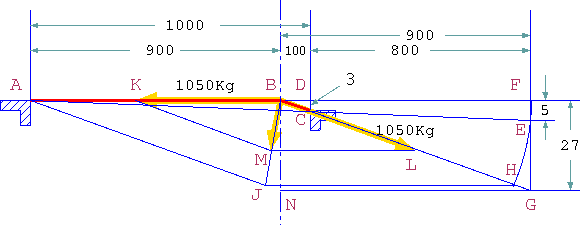 (図版178)
(図版178)
その算出経過は
BM : 27mm = 1050Kg : 900mm
従って
BM / 27 = 1050 / 900
31.5 / 5 (音) = 6.3Kg
6.3 / 3 (本) = 2.1Kg です。
しかし その中から
1050 = 5 x 3 x 70 ですから
一弦分として計算すると
また 27mm = (900 : 100) x 3mmから
(A)の式に (B)と(C)を代入すると
つまり
上下に100を掛けて
上下の900が消えて
となります。

上記の値を使い

と計算出来ます。
また 張力(T)は
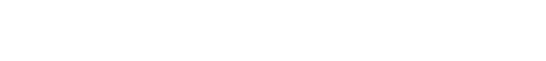
とも表されますので
(1)の式に代入すれば
したがって上記の5点が解れば 計算出来るように思われます。
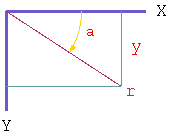 Fig-1
Fig-1
また 角度から算出する計算式を出して見ました。
ですので 高さ y は
前の (1)式に当てはめると 「l = r」また「h = y」ですので

l が無くなり
となります。
また (3)の式から
として 計算できます。
実際に測定するとして その測定誤差を考えます。
1度の差は 1.2Kg となり
また 糸を使って h を計る場合, 誤差は0.5mmぐらいかと思いますが
0.5mmの測定精度では 0.35Kgの誤差となります。