第7回 Beats (Inharmonicity) #7

インハーモニシティのある場合の“うなり”です。
まず 周波数を求めてみます。

function ifreq = getIfrequ(key,leng,bante,multi)
  inh = getInha(key, leng, bante);
  icent = calcInha(inh, multi);
  freq = getFrequ(key)*multi;
  ifreq = ctof(freq,icent);
end

function ih = calcInha(inh,multi)
  ih = inh*multi.*multi;
end

calcInha.mは インハーモニシティ値と倍数から 倍音のインハーモニシティ値を計算します。

> calcInha(0.5, [1 2 3])
ans =

   0.50000   2.00000   4.50000

getIfrequ.mは キー番号,弦長,番手,倍数から倍音の周波数を求めます。

> getIfrequ(37, 742.45, 16.5, [1 2 3])
ans =

   220.03   440.21   660.70

キー番号とキー間隔,弦長,番手から“うなり”を求めてみます。

function beat = getIbeat(key,inte,leng1,bante1,leng2,bante2)
  ratio = Interval(inte);
  freq1 = getIfrequ(key, leng1, bante1, ratio(2));
  freq2 = getIfrequ(key+inte, leng2, bante2, ratio(3));
  beat = freq2-freq1;
end

> getIbeat(37, 5, 742.45, 16.5, 581.81, 16.0)
ans =  0.65540

次に キー全体の“うなり”を求めてみます。

ただ 弦データからでは計算が繁雑になるので 全てのインハーモニシティ値を設定して行います。

function ih = makeCurve(wound, a49, grade)
  ks = [1:88]-wound; #（巻線数, ピッチ, 傾き）
  ih = cosh(grade.*ks);
  df = a49/ih(49);
  ih = ih.*df;
end

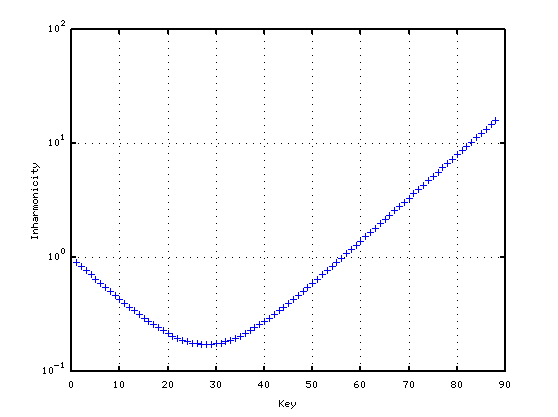
> inh = makeCurve(28, 0.55, 0.087)
> semilogy(inh, '@')
> grid on

2つを変更します。

function ifreq = getIHfrequ(key, multi, inh)
  icent = calcInha(inh, multi);
  freq = getFrequ(key)*multi;
  ifreq = ctof(freq, icent);
end

function beat = getIHbeat(key, ratio, inha)
  key2 = key+ratio(1);
  freq1 = getIHfrequ(key, ratio(2), inha(key));
  freq2 = getIHfrequ(key2, ratio(3), inha(key2));
  beat = freq2-freq1;
end

では シミュレーションしたインハーモニシティ値から キー全体の“うなり”を求めてみます。

function dispIbeats(intes)
  inha = makeCurve(28, 0.55, 0.087);
  for inte = intes
    ratio = Interval(inte);
    ks = 1:88-inte;
    beat = getIHbeat(ks, ratio, inha);
    plot(beat, '@')
    hold on
  end
  hold off
  xlabel('Key')
  ylabel('Beat')
end

> dispIbeats([5 7 12 24])
> grid on
> axis([0 90 -100 10])

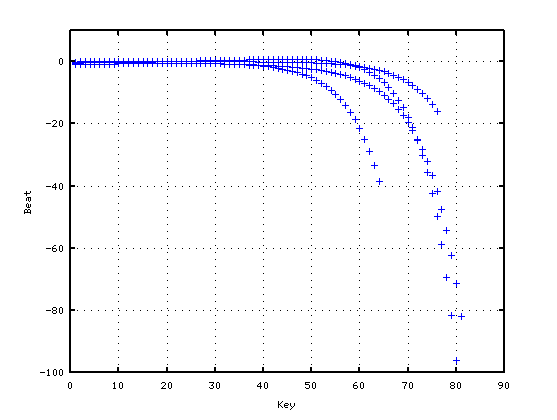
4度(5)・5度(7)・オクターブ(12)・2オクターブ(24)の“うなり”です。
しかしまだ Tuningのシミュレーションは行っていません。
そこで Tuningを行ってから キー全体の“うなり”を求めてみます。

function dispTune(intes)
  global Inha Cent KB;
  KB = 88;
  grade = 0.087;
  Inha = makeCurve(28, 0.55, grade);
  Cent = tuning_c(Inha, 1.0, grade);
  for inte = intes
    ratio = Interval(inte);
    ks = 1:KB-inte;
    beat = getIBeat(ks, ratio);
    plot(beat,'@')
    hold on
  end
  hold off
  xlabel('Key')
  ylabel('Beat')
end

function beat = getIBeat(key, ratio)
  freq1 = getIFrequ(key, ratio(2));
  freq2 = getIFrequ(key.+ratio(1), ratio(3));
  beat = freq2-freq1;
end

function ifreq = getIFrequ(key, multi)
  global Inha Cent;
  icent = calcInha(Inha(key), multi)+Cent(key);
  freq = getFrequ(key)*multi;
  ifreq = ctof(freq, icent);
end

> dispTune([5 7 12 24])
> grid on
> axis([0 90 -100 20])

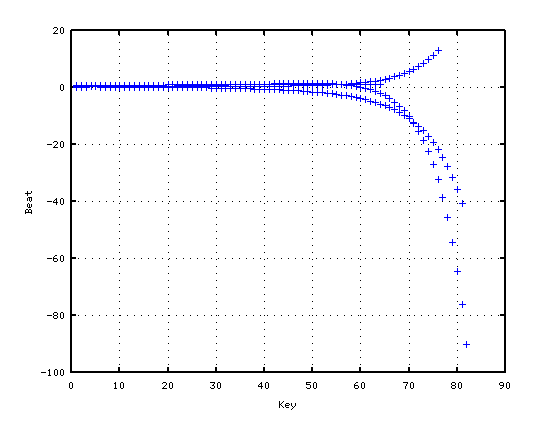
(tuning_c.m は省略)
さらに 画面に説明を加えます。

function dispTune1(intes)
  global Inha Cent KB;
  KB = 88;
  grade = 0.087;
  Inha = makeCurve(28,0.55,grade);
  Cent = tuning_c(Inha,1.0,grade);
  n = 1;
  for inte = intes
    [ratio name] = Interval(inte);
    ks = 1:KB-inte;
    beat = getIBeat(ks,ratio);
    str = strcat(';', name, ';@', getCP(n++));
    plot(beat, str)
    hold on
  end
  hold off
  grid on
  xlabel('Key')
  ylabel('Beat')
  axis([0 90 -40 20])
  legend(2)
end

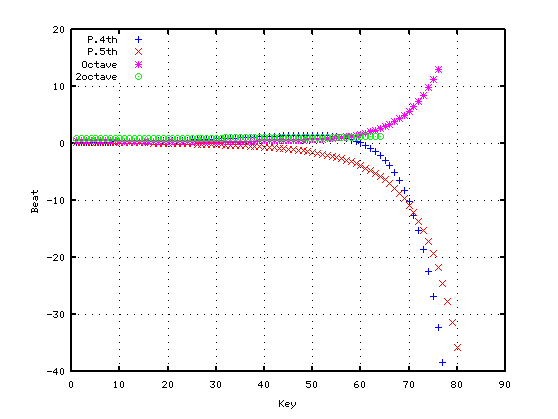
> dispTune1([5 7 12 24])