等分平均律の可能性 (Equal Temperament) v1.3.1

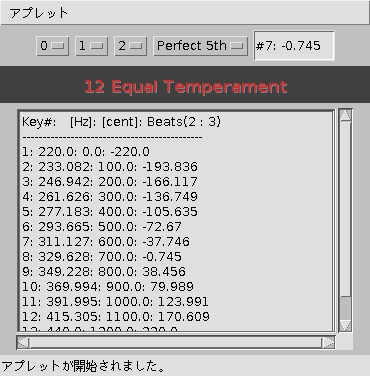
12等分平均律の性質として 5度音程の`うなり'（例えば A(37)220[Hz] - E(44)329.6276[Hz] で -0.7448）は少ないけれども 長3度（A(37) - Cis(41) 277.1826[Hz] で 8.7305）では多過ぎると言われています。

そこで 過去の音律に解決を求めたり 全く別の新しい音律を創る試みが なされたりしています。

そうした中「19等分平均律」（※１）がありましたので ここでは1オクターブを 平均に（12√の12の値を変更して等倍に）分割して その周波数を求めて 純正の音程比の`うなり'を見ることにします。

(Java appletは 利用出来なくなりました；)

＞ JavaScript版です。

使い方：

• (※ 変更箇所：
  v1.3.1['16/04/13] Javaアプレットをボタンで動作するように変更しました。
  v1.3['14/01/12] 計算方法を一部修正しました。 JavaScript版を追加しました。 cssファイルを追加しました。
  v1.2.1['10/11/05] (説明文を追加しました。)
  v1.2['05/11/26] 計算方法を変更しました。
  v1.1 (※)最小値のキー分割数と 値'うなり'の数を表示しました。 音程比を増加しました。999等分までとなりました。)

• 左の[ 0 ]で 100の位を 中の[ 1 ]で 10の位を 右の[ 2 ]で 1の位をセットして 等分平均律の分割数を選びます。 （999等分まで可能です。）

• 右の[ Perfect 5th ]で調べる音程(Interval)を選びます。

• (※)[ #7:-0.7448 ]上記の音程で最小になる Key番号分割番号と 'うなり'の数を表示します。

• (※)下のテキスト画面に 基準音 A(27)220[Hz]から1オクターブ分で 分割された音程番号(Key番号)分割番号 :周波数[Hz]:セント値[cent]： そしてその Keyで上記の「音程比」 での'うなり'の数を表示します。

• 音程比：
  1. minor 2nd [16 : 15]
  2. Major 2nd [9 : 8]
  3. minor 3rd [6 : 5]
  4. Major 3rd [5 : 4]
  5. Perfect 4th [4 : 3]
  6. (※)Dim. 5th [7 : 5]
  7. Perfect 5th [3 : 2]
  8. minor 6th [8 : 5]
  9. Major 6th [5 : 3]
  10. (※)minor 7th [9 : 5]
  11. Major 7th [15 : 8]

1. 純正律の周波数・セント値（短3度(m-3)・長3度(M-3)・完全5度(p-5)）

         [Hz] :  [cent]
   m-3> 264.0 : 315.641
   M-3> 275.0 : 386.314
   p-5> 330.0 : 701.955

2. 12平均律 (100.0セント差)

      Key#:     [Hz] :   [cent] : Beats
   m-3>3. : 261.6255 : 300.0    : -11.872
   M-3>4. : 277.1826 : 400.0    : 8.73052
   p-5>7. : 329.6275 : 700.0    : -0.7448

3. 18平均律（最小値と前後の値を見ます。(66.6666セント差)）

   m-3>4. : 256.6363 : 266.6666 : -36.818
   m-3>5. : 266.7117 : 333.3333 : 13.5586
   m-3>6. : 277.1826 : 400.0    : 65.9131
   
   M-3>5. : 266.7117 : 333.3333 : -33.153
   M-3>6. : 277.1826 : 400.0    : 8.73052
   M-3>7. : 288.0646 : 466.6666 : 52.2584
   
   p-5>10 : 323.3415 : 666.6666 : -13.316
   p-5>11 : 336.0357 : 733.3333 : 12.0714
   p-5>12 : 349.2282 : 800.0    : 38.4564

4. 19平均律（5度がミーントーンの 696.5784[cent]に近い。(63.15789セント差)）

   m-3>5. : 264.0226 : 315.7894 : 0.11299
   M-3>6. : 273.8323 : 378.9473 : -4.6705
   p-5>11 : 328.6269 : 694.7368 : -2.7460

5. 31平均律（長3度が小さく、短3・5度も少ない方です。(38.71セント差)）

   m-3>8. : 263.0921 : 309.6774 : -4.5393
   M-3>10 : 275.1244 : 387.0967 : 0.49765
   p-5>18 : 329.0139 : 696.7741 : -1.9721

6. 34平均律（316.641 386.314 701.955 の近似値 315 385 700 の最大公約 数(35)に近い 35.294セント差）

   m-3>9. : 264.3060 : 317.6470 : 1.53021
   M-3>11 : 275.3054 : 388.2352 : 1.22162
   p-5>20 : 330.7494 : 705.8823 : 1.49892

7. 53平均律（純正調オルガンの製作者 田中 正平博士が提案(22.6415セント差)）

   m-3>14 : 264.2044 : 316.9811 : 1.02197
   M-3>17 : 274.7764 : 384.9056 : -0.8942
   p-5>31 : 329.9869 : 701.8867 : -0.0260

8. 99平均律（12.1212セント差）

   m-3>26 : 263.9253 : 315.1515 : -0.3733
   M-3>32 : 275.2487 : 387.8787 : 0.99487
   p-5>58 : 330.2050 : 703.0302 : 0.41006

等が 3つの`うなり'の少ない等分平均律ですが それが調律出来るものかは分かりません；

m-3>5. : 254.1775 : 250.0    : -49.112
m-3>6. : 261.6255 : 300.0    : -11.872
m-3>7. : 269.2917 : 350.0    : 26.4588

M-3>7. : 269.2917 : 350.0    : -22.832
M-3>8. : 277.1826 : 400.0    : 8.73052
M-3>9. : 285.3046 : 450.0    : 41.2188

p-5>13 : 320.2437 : 650.0    : -19.512
p-5>14 : 329.6275 : 700.0    : -0.7448
p-5>15 : 339.2863 : 750.0    : 18.5727

しかし 50セントの差は 最小値は12平均律の値となり `うなり'の減少効果ではなさそうです。

m-3>7. : 258.6205 : 280.0    : -26.897
m-3>8. : 264.6654 : 320.0    : 3.32753
m-3>9. : 270.8517 : 360.0    : 34.2588

M-3>9. : 270.8517 : 360.0    : -16.592
M-3>10 : 277.1826 : 400.0    : 8.73052
M-3>y11 : 283.6614 : 440.0    : 34.6458

p-5>17 : 325.8414 : 680.0    : -8.3170
p-5>18 : 333.4576 : 720.0    : 6.91528
p-5>19 : 341.2518 : 760.0    : 22.5036

40セント差も `うなり'の減少効果はないように見受けられます。

• （※１）十九平均律の可能性 - 音律再考 別宮 貞雄 音楽芸術 第44巻 8号 1986年
• 十九平均律と十八平均律 - 別宮貞雄氏への手紙 戸田 邦雄 音楽芸術 第44巻 11号 1986年
• 音律再々考 - 19平均律解説 別宮 貞雄 音楽芸術 第45巻 3号 1987年